新一届中央领导集体非常重视勤俭节约，从“光盘行动”到“节约办春晚”。到饭店吃饭是吃光盘子或时打包带走，称为“光盘族”，否则称为“非光盘族”．政治课上政治老师选派几位同学组成研究性小组，从某社区[25,55]岁的人群中随机抽取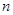人进行了一次调查，得到如下统计表：

组数	分组	频数	频率	光盘族占本组比例
第1组	[25,30）	50	0．05	30%
第2组	[30,35）	100	0．10	30%
第3组	[35,40）	150	0．15	40%
第4组	[40,45）	200	0．20	50%
第5组	[45,50）	a	b	65%
第6组	[50,55）	200	0．20	60%

 
（1）求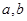的值，并估计本社区[25,55）岁的人群中“光盘族”所占比例；
（2）从年龄段在[35,45）的“光盘族”中采用分层抽样方法抽取8人参加节约粮食宣传活动，并从这8人中选取2人作为领队．求选取的2名领队分别来自[35,40）与[40,45）两个年龄段的概率。

科目 数学   题型 解答题   难度 中等

知识点： 随机抽样 误差估计