(本小题满分12分)
已知函数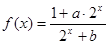 是奇函数,并且函数
是奇函数,并且函数 的图像经过点
的图像经过点 .
.
(Ⅰ)求实数 的值;
的值;
(Ⅱ)求函数 在
在 时的值域.
时的值域.
已知数列 中,
中,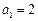 ,且
,且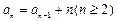 ,求这个数列的第m项
,求这个数列的第m项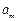 的值
的值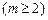 .现给出此算法流程图的一部分如图。
.现给出此算法流程图的一部分如图。
(1)请将空格部分(两个)填上适当的内容;
(2)用“For”循环语句写出对应的算法;
(3)若输出S=16,则输入的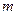 的值是多少?
的值是多少?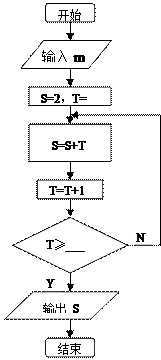
教室内有5个学生,分别佩戴1号到5号的校徽,任选3人记录他们的校徽号码。
(1)求最小号码为2的概率;(2)求三个号码中至多有一个偶数的概率
已知数列 的各项均为正数,观察程序框图,若
的各项均为正数,观察程序框图,若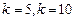 时,分别有
时,分别有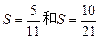 .
.
(1)试求数列 的通项;
的通项;
(2)令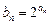 ,求
,求 的值.
的值.
如图,已知向量 ,可构成空间向量的一个基底,若
,可构成空间向量的一个基底,若
 ,在向量已有的运算法则的基础上,新定义一种运算
,在向量已有的运算法则的基础上,新定义一种运算 ,显然
,显然 的结果仍为一向量,记作
的结果仍为一向量,记作 .
.
1、求证:向量 为平面
为平面 的法向量;
的法向量;
2、求证:以 为边的平行四边形
为边的平行四边形 的面积等于
的面积等于 ;
;
将四边形 按向量
按向量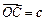 平移,得到一个平行六面体
平移,得到一个平行六面体 ,试判断平行六面体的体积
,试判断平行六面体的体积 与
与 的大小.
的大小.
如图,在三棱锥 中,
中,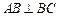 ,
, ,点
,点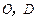 分别是
分别是 的中点,
的中点, 底面
底面 .
.
(1)求证: 平面
平面 ;
;
(2)当 时,求直线
时,求直线 与平面
与平面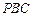 所成角的余弦值;
所成角的余弦值;
(3)当 为何值时,
为何值时, 在平面
在平面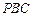 内的射影恰好为
内的射影恰好为 的重心?
的重心?