问题背景：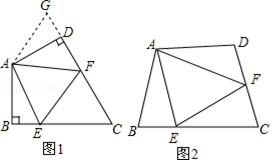
（1）如图1：在四边形ABCD中，AB=AD，∠BAD=120°，∠B=∠ADC=90°．E，F分别是BC，CD上的
点．且∠EAF=60°．探究图中线段BE，EF，FD之间的数量关系．小王同学探究此问题的方法是，延长FD到点G．使DG=BE．连结AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是 _____
探索延伸：
（2）如图2，若在四边形ABCD中，AB=AD，∠B+∠D=180°．E，F分别是BC，CD上的点，且∠EAF=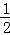
∠BAD，上述结论是否仍然成立，并说明理由；
在抗震救灾活动中，某厂接到一份订单，要求生产7200顶帐篷支援四川灾区，后来由于情况紧急，接收到上级指示，要求生产总量比原计划增加20%，且必须提前4天完成生产任务，该厂迅速加派人员组织生产，实际每天比原计划每天多生产720顶，请问该厂实际每天生产多少顶帐篷？
下表给出1980年至今的百米世界记录情况：
| 国籍 |
姓名 |
成绩（秒） |
日期 |
国籍 |
姓名 |
成绩（秒） |
日期 |
| 牙买加 |
博尔特 |
9.72 |
2008．6．1 |
美国 |
格林 |
9.79 |
1999．6．16 |
| 牙买加 |
鲍威尔 |
9.74 |
2007．9．9 |
加拿大 |
贝利 |
9.84 |
1996．7．27 |
| 牙买加 |
鲍威尔 |
9.77 |
2006．8．18 |
美国 |
伯勒尔 |
9.85 |
1994．6．7 |
| 牙买加 |
鲍威尔 |
9.77 |
2006．6．11 |
美国 |
刘易斯 |
9.86 |
1991．8．25 |
| 美国 |
加特林 |
9.77 |
2006．5．12 |
美国 |
伯勒尔 |
9.90 |
1991．6．14 |
| 牙买加 |
鲍威尔 |
9.77 |
2005．6．14 |
美国 |
刘易斯 |
9.92 |
1988．9．24 |
| 美国 |
蒙哥 马利 |
9.78 |
2002．9．14 |
美国 |
史密斯 |
9.93 |
1983．7．3 |
（1）请你根据以上成绩数据，求出该组数据的众数为 ，极差为 ．
（2）请在下图中用折线图描述此组数据．
在我市迎接奥运圣火的活动中，某校教学楼上悬挂着宣传条幅DC，小丽同学在点A处，测得条幅顶端D的仰角为30°，再向条幅方向前进10米后，又在点B处测得条幅顶端D的仰角为45°，已知测点A、B和C离地面高度都为1.44米，求条幅顶端D点距离地面的高度．（计算结果精确到0.1米，参考数据：
．）
解不等式组：
．
计算：
；