数学课上老师出了一道题:计算2962的值,喜欢数学的小亮举手做出这道题,他的解题过程如下:2962=(300-4)2=3002-2×300×(-4)+42=90000+2400+16=92416
老师表扬小亮积极发言的同时,也指出了解题中的错误,你认为小亮的解题过程错在哪儿,并给出正确的答案.
如图,在Rt△ABC中,∠B=90°3,∠,C=30°BC="5" .点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
(1)求证:AE=DF;
(2)△DEF能够成为等边三角形吗?如果能,求出相应的t值;如果不能,说明现由.
(3)当t为何值时,△DEF为直角三角形?请说明理由.
直线y=x+b与x轴交于点C(4,0),与y轴交于点B,并与双曲线y= (x<0)交于点A(-1,n).
(x<0)交于点A(-1,n).
(1)求直线与双曲线的解析式.
(2)连接OA,求∠OAB的正弦值.
(3)若点D在x轴的正半轴上,是否存在以点D、C、B构成的三角形与△OAB相似?若存在求出D点的坐标,若不存在,请说明理由.
某校学生捐款支援地震灾区,第一次捐款总额为6600元,第二次捐款总额为7260元,第二次捐款人数比第一次多30人,而且两次人均捐款额恰好相等.求第一次的捐款人数.
已知:如图,AB与⊙O相切于点C,OA=OB,⊙O的直径为4,AB=8.求sinA的值.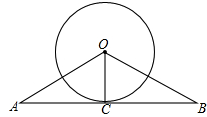
已知:如图,点A,C,D,B在同一条直线上,AC=BD,AE=BF,∠A=∠B.求证:∠E=∠F.