如图,点D为码头,A,B两个灯塔与码头的距离相等,DA,DB为海岸线.一 轮船离开码头,计划沿∠ADB的角平分线航行,在航行途中C点处,测得轮船与灯塔A和灯塔B的距离相等.试问:轮船航行是否偏离指定航线?请说明理由.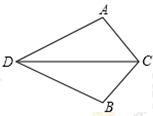
已知:如图,在△ABC中,∠ACB=90°,AC=BC,D是AB的中点,点E在AC上,点F在BC上,且AE=CF.
(1)求证:DE=DF,DE⊥DF;
(2)若AC=4,求四边形DECF面积.
如图,在安大公路(直线BD)的同侧有两个气象信息采集点A、E ,点A、E到安大公路的距离AB=12、 ED=3,两垂足间的距离BD=20.
(1)在线段BD上找一点C,铺设线路AC、CE,要使AC+CE最小,请在图中作出点C;
(2)求出AC+CE的最小值.
如图,已知△ABC的三个顶点在格点上.
(1)△ABC的三边中长度为 的边为__________;
的边为__________;
(2)作出与△ABC关于x轴对称的△A1B1C1;
(3)写出下列点的坐标:A1(______,_______)B1(_______,_______)C1(_______,_______).
如图,已知:△ABC中,AB=AC,M是BC的中点,D、E分别是AB、AC边上的点,且BD=CE.求证:MD=ME.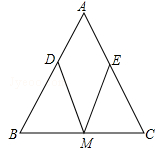
如图,已知:大风把一颗大树刮断,折断的一端恰好落在地面上的A处,量得BC=6m,AC=8m,试计算这棵大树的高度.