某商场要经营一种新上市的文具,进价为20元/件.试营销阶段发现:当销售单价25元/件时,每天的销售量是250件;销售单价每上涨1元,每天的销售量就减少10件.
(1)写出商场销售这种文具,每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式.
(2)求销售单价为多少元时,该文具每天的销售利润最大?
(3)商场的营销部结合上述情况,提出了A,B两种营销方案:
方案A:该文具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件文具的利润至少为25元.
请比较哪种方案的最大利润更高,并说明理由.
计算或化简:
(1)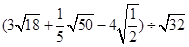 (2)
(2) 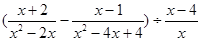
如图①,△ABC与△DEF为等腰直角三角形,CB与EF重合,AC=DE=8,∠ACB=∠DEF=90°固定△ABC,将△DEF绕点C顺时针旋转,当边FE与边CA重合时,旋转终止。设FE、FD(或它的延长线)分别交AB(或它的延长线)于点P、Q,如图②
(1)问:始终与△CPB相似的三角形(不添加其他辅助线)有①及②
(2)设BP=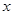 ,AQ=
,AQ=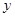 ,求
,求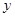 关于
关于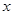 的函数关系式;
的函数关系式;
(3)问:当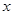 为何值时,△CPQ是等腰三角形?
为何值时,△CPQ是等腰三角形?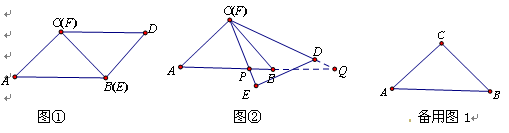
有一块直角三角形木板如图所示,已知∠C=90°,BC=3cm, AC=4cm.根据需要,要把它加工成一个正方形木板,小明和小丽分别设计了如图1和图2的两种方法,哪一块正方形木板面积更大?请说明理由.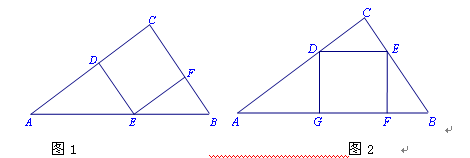
某商店准备从机械厂购进甲、乙两种零件进行销售,若每个甲零件的进价比每个乙种零件的进价少2元,且用80元购进甲种零件的数量与用100元购进乙种零件的数量相同。
(1)求甲、乙两种零件每个的进价分别为多少元?
(2)若该商店本次购进甲种零件的数量比购进乙种零件的数量的3倍还少5个,购进两种零件的总数量不超过95个,将本次购进的甲、乙两种零件全部售出后,可使销售两种零件的销售价格均为12元,则将本次购进的甲、乙两种全部售出后,可使销售两种零件的总利润(利润=售价-进价)超过302元,通过计算求出该商店本次从机械厂购进甲、乙两种零件有几种方案?请你设计出来。
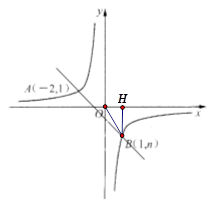
如图,一次函数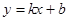 的图象与反比例函数
的图象与反比例函数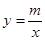 的图象相交于A、B两点.
的图象相交于A、B两点.
(1)利用图中条件,求反比例函数与一次函数的关系式;
(2)根据图象写出使该一次函数的值大于该反比例函数的值的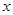 的取值范围;
的取值范围;
(3)过B点作BH垂直于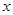 轴垂足为H,连接OB,在
轴垂足为H,连接OB,在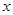 轴是否存在一点P(不与点O重合),使得以P、B、H为顶点的三角形与△BHO相似;若存在,直接写出点P的坐标;不存在,说明理由。
轴是否存在一点P(不与点O重合),使得以P、B、H为顶点的三角形与△BHO相似;若存在,直接写出点P的坐标;不存在,说明理由。