(本小题满分10分)某公司研制出一种新颖的家用小电器,每件的生产成本为18元,经市场调研表明,按定价40元出售,每日可销售20件.为了增加销量,每降价1元,日销售量可增加2件.问将售价定为多少元时,才能使日利润最大?求最大利润.
解方程:(每小题5分,共10分)
① 3x-7(x-1)=3-2(x+3)
②
已知:如图,△ABC中,点D是BC边上的一点,∠ADE=∠ABC=60°,DE交∠ABC的外角平分线于点E.求证:△ADE是等边三角形.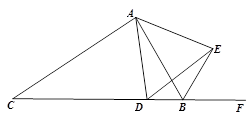
已知:如图,在△ABC中,点D是BC的中点,过点D作直线交AB,CA的延长线于点E,F.当BE=CF时,求证:AE=AF.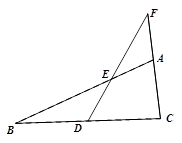
如图,四边形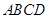 中,
中,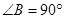 ,
,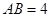 ,
,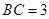 ,
,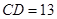 ,
,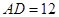 ,求四边形
,求四边形 的面积.
的面积.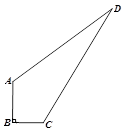
为了进一步落实“节能减排”措施,冬季供暖来临前,某单位决定对9000平方米的“外墙保温”工程进行招标,现有甲、乙两个工程队参与投标,比较这两个工程队的标书发现:乙队每天完成的工程量是甲队的1.5倍,这样乙队单独干比甲队单独干能提前15天完成任务.问甲队每天完成多少平方米?