(本小题满分10分)在一个不透明的口袋里装有分别标有数字-3、-1、0、2的四个小球,除数字不同外,小球没有任何区别,每次试验先搅拌均匀.
(1)从中任取一球,求抽取的数字为正数的概率;
(2)从中任取一球,将球上的数字记为a,求关于x的一元二次方程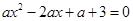 有实数根的概率;
有实数根的概率;
(3)从中任取一球,将球上的数字作为点的横坐标记为x(不放回);在任取一球,将球上的数字作为点的纵坐标,记为y,试用画树状图(或列表法)表示出点(x,y)所有可能出现的结果,并求点(x,y)落在第二象限内的概率.
(2014年江西抚州10分)如图,抛物线y=ax2+2ax(a<0)位于x轴上方的图象记为F1,它与x轴交于P1、O两点,图象F2与F1关于原点O对称,F2与x轴的另一个交点为P2,将F1与F2同时沿x轴向右平移P1P2的长度即可得到F3与F4;再将F3与F4同时沿x轴向右平移P12P的长度即可得到F5与F6;…;按这样的方式一直平移下去即可得到一系列图象F1,F2,…,Fn.我们把这组图象称为“波浪抛物线”.
(1)当a=﹣1时,①求图象F1的顶点坐标;②点H(2014,﹣3) (填“在”或“不在”)该“波浪抛物线”上;若图象Fn的顶点Tn的横坐标为201,则图象Fn对应的解析式为 ,其自变量x的取值范围为 .
(2)设图象Fn、Fn+1的顶点分别为Tn、Tn+1(m为正整数),x轴上一点Q的坐标为(12,0).试探究:当a为何值时,以O、Tn、Tn+1、Q四点为顶点的四边形为矩形?并直接写出此时m的值.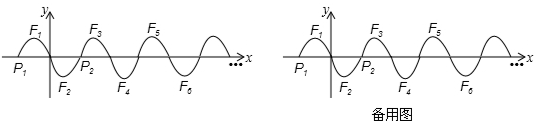
(2014年吉林省10分)如图①,直线l:y=mx+n(m>0,n<0)与x,y轴分别相交于A,B两点,将△AOB绕点O逆时针旋转90°,得到△COD,过点A,B,D的抛物线P叫做l的关联抛物线,而l叫做P的关联直线.
(1)若l:y=﹣2x+2,则P表示的函数解析式为 ;若P:y=﹣x2﹣3x+4,则l表示的函数解析式为 .
(2)求P的对称轴(用含m,n的代数式表示);
(3)如图②,若l:y=﹣2x+4,P的对称轴与CD相交于点E,点F在l上,点Q在P的对称轴上.当以点C,E,Q,F为顶点的四边形是以CE为一边的平行四边形时,求点Q的坐标;
(4)如图③,若l:y=mx﹣4m,G为AB中点,H为CD中点,连接GH,M为GH中点,连接OM.若OM=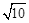 ,直接写出l,P表示的函数解析式.
,直接写出l,P表示的函数解析式.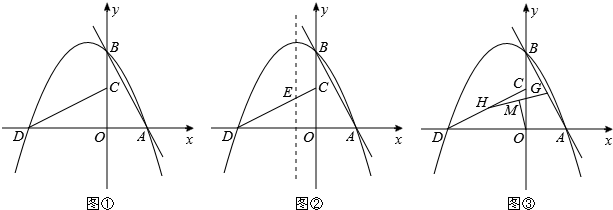
(年湖北黄石10分)如图,在矩形ABCD中,把点D沿AE对折,使点D落在OC上的F点,已知AO=8.AD=10.
(1)求F点的坐标;
(2)如果一条不与抛物线对称轴平行的直线与该抛物线仅有一个交点,我们把这条直线称为抛物线的切线,已知抛物线经过点O,F,且直线y=6x﹣36是该抛物线的切线,求抛物线的解析式;
(3)直线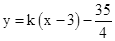 与(2)中的抛物线交于P、Q两点,点B的坐标为(3,
与(2)中的抛物线交于P、Q两点,点B的坐标为(3,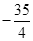 ),求证:
),求证: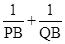 为定值.(参考公式:在平面直角坐标系中,若M(x1,y1),N(x2,y2),则M,N两点间的距离为|MN|=
为定值.(参考公式:在平面直角坐标系中,若M(x1,y1),N(x2,y2),则M,N两点间的距离为|MN|=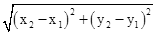 ).
).
(年贵州黔西南12分)已知点P(x0,y0)和直线y=kx+b,则点P到直线y=kx+b的距离d可用公式 计算.
计算.
例如:求点P(﹣2,1)到直线y=x+1的距离.
解:因为直线y=x+1可变形为x﹣y+1=0,其中k=1,b=1.
所以点P(﹣2,1)到直线y=x+1的距离为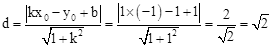 .
.
根据以上材料,求:
(1)点P(1,1)到直线y=3x﹣2的距离,并说明点P与直线的位置关系;
(2)点P(2,﹣1)到直线y=2x﹣1的距离;
(3)已知直线y=﹣x+1与y=﹣x+3平行,求这两条直线的距离.
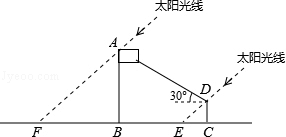
(年贵州六盘水14分)为践行党的群众路线,六盘水市教育局开展了大量的教育教学实践活动,如图是其中一次“测量旗杆高度”的活动场景抽象出的平面几何图形.
活动中测得的数据如下:
①小明的身高DC=1.5m
②小明的影长CE=1.7cm
③小明的脚到旗杆底部的距离BC=9cm
④旗杆的影长BF=7.6m
⑤从D点看A点的仰角为30°
请选择你需要的数据,求出旗杆的高度.(计算结果保留到0.1,参考数据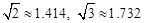 ,)
,)