如图四边形ABCD中,AD∥BC,DE平分∠ADB,∠BDC=∠BCD.
(1)求证:∠1+∠2=900.
(2)如图2,若∠ABD的平分线与CD的延长经交于点F,且∠F=600,求∠ABC的度数.
.如图,在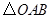 中,
中,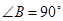 ,
,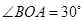 ,
,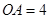 ,将
,将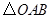 绕点
绕点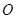 按逆时针方向旋转至
按逆时针方向旋转至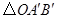 ,
,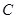 点的坐标为(0,4).
点的坐标为(0,4).(1)求
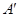 点的坐标;
点的坐标;(2)求过
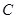 ,
,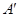 ,
,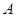 三点的抛物线
三点的抛物线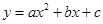 的解析式;
的解析式;(3)在(2)中的抛物线上存在点
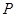 ,使以
,使以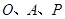 为顶点的三角形是等腰直角三角形.请直接写出点
为顶点的三角形是等腰直角三角形.请直接写出点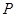 的坐标.
的坐标.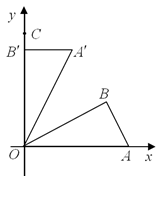
百货商店服装柜台在销售中发现,“乐乐”牌童装平均每天可售20件,每件赢利40元,为了迎接“六一”儿童节,商场决定采取适当的降价措施,扩大销售量,增加赢利,减少库存。经市场调查发现:如果每件童装降价4元,那么平均每天可多售8件,要想平均每天在销售这种童装上赢利1200元,那么每件童装应降价多少元?
用长为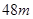 的绳子,围成矩形场地,矩形的一边长为
的绳子,围成矩形场地,矩形的一边长为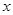 m,面积为
m,面积为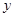 m
m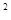 .
.(1)求
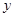 与
与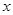 之间的函数关系式,并指出
之间的函数关系式,并指出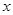 的取值范围;
的取值范围;(2)当
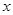 为多少时,矩形面积最大,最大面积是多少.
为多少时,矩形面积最大,最大面积是多少.
如图,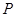 是正三角形
是正三角形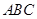 内的一点,且
内的一点,且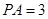 ,
, 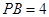 ,
,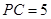 .若将
.若将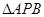 绕点
绕点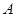 逆时针旋转后,得到
逆时针旋转后,得到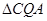 .
.(1)求点
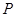 与点
与点 之间的距离;
之间的距离;(2)求
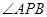 的度数.
的度数.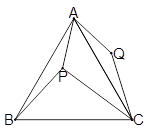
.如图,在平行四边形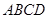 中,过点
中,过点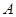 作
作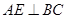 ,垂足为
,垂足为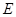 ,连接
,连接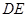 ,
,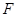 为线段
为线段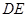 上一点,且
上一点,且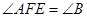 .
.(1)求证:
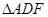 ∽
∽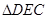 ;
;(2)若
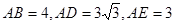 ,求
,求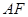 的长.
的长.