(本题6分)某商场将进货价为30元的台灯以40元的销售价售出,平均每月能售出600个.市
场调研表明:当销售价每上涨1元时,其销售量就将减少10个.若设每个台灯的销售价上涨a元.
(1)试用含a的代数式填空:
①涨价后,每个台灯的销售价为_______元;
②涨价后,每个台灯的利润为_______元;
③涨价后,商场的台灯平均每月的销售量为_______台.
(2)如果商场要想销售利润平均每月达到10000元,商场经理甲说“在原售价每台40元的基础上再上涨40元,可以完成任务”,商场经理乙说“不用涨那么多,在原售价每台40元的基础上再上涨10元就可以了”,试判断经理甲与乙的说法是否正确,并说明理由.
解不等式组: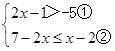
如图,在矩形ABCD中,点P在边CD上,且与C、D不重合,过点A作AP的垂线与CB的延长线相交于点Q,连接PQ,M为PQ中点.
(1)求证:△ADP∽△ABQ;
(2)若AD=10,AB=20,点P在边CD上运动,设DP=x,BM2=y,求y与x的函数关系式,并求线段BM的最小值;
(3)若AD=10,AB=a,DP=8,随着a的大小的变化,点M的位置也在变化.当点M落在矩形ABCD外部时,求a的取值范围.
焚烧秸秆是造成雾霾的重要原因,某单位在科研部门的支持下,研发了一套设备,把秸秆转化为一种化工原料.已知该套设备每月的处理量最少为400吨,最多为600吨,月处理成本y(元)与月处理量x(吨)的函数关系为:y= x2-200x+80000,且每处理一吨秸秆得到的化工原料价值为100元.
x2-200x+80000,且每处理一吨秸秆得到的化工原料价值为100元.
(1)设每月获利为S元,求S(元)与x(吨)之间的函数关系式.
(2)该单位每月能否获利?如果获利,求出最大利润;如果不获利,则国家至少需要补贴多少元才能使该单位不亏损?
某中学对本校学生每天完成作业所用时间的情况进行抽样调查,随机调查了九年级部分学生每天完成作业所用的时间,并把统计结果制作成如图所示的频数分布直方图(时间取整数,图中从左至右依次为第一、二、三、四、五组)和扇形统计图.请结合图中信息解答下列问题.
(1)本次调查的学生人数为人;
(2)补全频数分布直方图;
(3)根据图形提供的信息判断,下列结论正确的是(只填所有正确结论的代号);
| A.由图(1)知,学生完成作业所用时间的中位数在第三组内 |
| B.由图(1)知,学生完成作业所用时间的众数在第三组内 |
| C.图(2)中,90~120数据组所在扇形的圆心角为108° |
| D.图(1)中,落在第五组内数据的频率为0.15 |
(4)学生每天完成作业时间不超过120分钟,视为课业负担适中.根据以上调查,估计该校九年级560名学生中,课业负担适中的学生约有多少人?
给出下列命题:
命题1:点(1,1)是直线y=x与双曲线y= 的一个交点;
的一个交点;
命题2:点(2,4)是直线y=2x与双曲线y= 的一个交点;
的一个交点;
命题3:点(3,9)是直线y=3x与双曲线y= 的一个交点;
的一个交点;
(1)请观察上面命题,猜想出命题n(n是正整数);
(2)证明你猜想的命题n是正确.