（本题9分）一只甲虫在5×5的方格（每小格边长为1m）上沿着网格线运动。它从A处出发去看望B、C、D处的其它甲虫（A,B,C,D都在格点上）。规定：向上向右走为正，向下向左走为负。若从A到B记为：A→B(＋1，＋4)，则从B到A记为：A→B(－1，－4)，其中第一个数表示左右方向，第二个数表示上下方向，那么图中
（1）图中A→C（ ， ），B→C（ ， ）, C→ （＋1， ）；
（2）若这只甲虫的行走路线为A→D→B→C，请计算该甲虫走过的路程；
（3）若这只甲虫从A处去甲虫P处的行走路线依次为（＋2，＋1），（＋3，＋4），（－3，-2），（+1，－2），请在图中标出P的位置
|
；若甲虫每走1m需消耗1．5焦耳的能量,则甲虫从A走到P的过程中共需消耗多少焦耳的能量?
如图所示，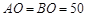
cm，OC是一条射线，OC⊥AB于点O，一只甲虫由点A以2cm/s的速度向B爬行，同时另一只甲虫由点O以3cm/s的速度沿OC方向爬行，是否存在这样的时刻，使两只甲虫与点O组成的三角形的面积为450cm2？若存在，请说明在什么时刻；若不存在，请说明理由。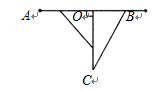
如图，AB是⊙O的直径，∠BAC的平分线AQ交BC于点P，交⊙O于点Q。已知AC=6，∠AQC=30度。
（1）求AB的长；
（2）求点P到AB的距离。
将如图所示的版面数字分别是1，2，3，4的四张扑克牌背面朝上，洗匀后放在桌面上（“A”看做是“1”）。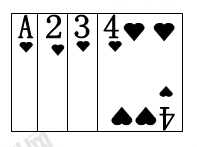
（1）从中随机抽出一张牌，牌面数字是偶数的概率是；
（2）从中随机抽出两张牌，两张牌面数字的和是5的概率是；
（3）先从中随机抽出一张牌，将牌面数字作为十位上的数字，然后将该牌放回并重新洗匀，再随机抽取一张，将牌面数字作为个位上的数字，请用画树形图的方法求组成的两位数恰好是4的倍数的概率。
如图，A、B为是⊙O上两点，C、D分别在半径OA、OB上，若AC=BD，求证：AD=BC。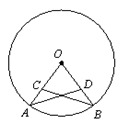
如图，四边形ABCD是边长为4的正方形，且DE＝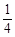
AB，△ABF是△ADE的旋转图形。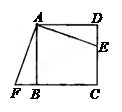
（1）旋转中心是哪一点？
（2）旋转了多少度？
（3）AF的长度是多少？
（4）如果连结EF，那么△AEF是怎样的三角形？