如图,AB是⊙O的直径,∠BAC的平分线AQ交BC于点P,交⊙O于点Q。已知AC=6,∠AQC=30度。
(1)求AB的长;
(2)求点P到AB的距离。
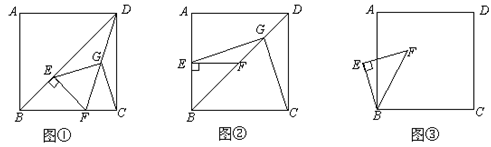
已知:如图①,正方形ABCD中,E为对角线BD上一点,
过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.(1)求证:EG=CG;
(2)将图①中△BEF绕B点逆时针旋转45º,如图②所示,取DF中点G,连接EG,CG.问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
(3)将图①中△BEF绕B点旋转任意角度,如图③所示,再连接相应的线段,问(1)中的结论是否仍然成立?通过观察你还能得出什么结论?(均不要求证明)
如图,在直角坐标平面内,函数 (
( ,
,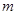 是常数)的图象经过
是常数)的图象经过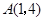 ,
,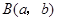 ,其中
,其中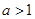 .过点
.过点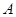 作
作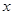 轴垂线,垂足为
轴垂线,垂足为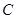 ,过点
,过点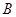 作
作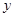 轴垂线,垂足为
轴垂线,垂足为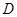 ,连结
,连结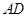 ,
,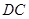 ,
,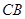 .
.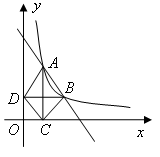
(1)若
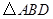 的面积为4,求点
的面积为4,求点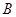 的坐标;
的坐标;(2)若
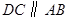 ,当
,当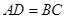 时,求直线
时,求直线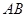 的函数的解析式.
的函数的解析式.
在长方形中画出5条线,把它分成的块数与画线的方式有直接关系.按如图1的方式画线,可以把它分成10块.(1)请你在图2中画出5条线,使得把这个长方形分成的块数最少(重合的线只看做一条),最少可分成块;
(2)请你在图2中画出5条线,使得把这个长方形分成的块数最多,最多可分成块.
(画出图形不写画法和理由)
甲、乙两支篮球队在集训期内进行了五场比赛,将比赛成绩进行统计后,绘制成如图1、图2的统计图.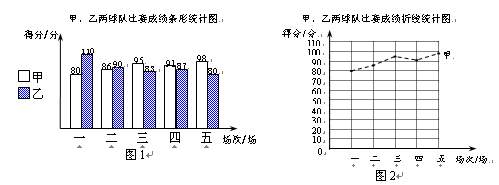
(1)在图12-2中画出折线表示乙队在集训期内这五场比赛成绩的变化情况
(2)已知甲队五场比赛成绩的平均分
 =90分,请你计算乙队五场比赛成绩的平均分
=90分,请你计算乙队五场比赛成绩的平均分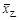 ;
;(3)如果从甲、乙两队中选派一支球队参加篮球锦标赛,根据上述统计情况,你认为选派哪支球队参赛更能取得好成绩?
如图,在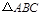 中,
中,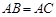 ,以AB为直径的
,以AB为直径的 交BC于点D,DE⊥AC于点E.
交BC于点D,DE⊥AC于点E.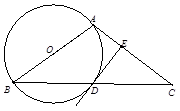
(1)求证DE是
 的切线;
的切线;(2)若∠BAC=120°,AB=2,求△DEC的面积.