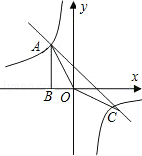
已知：如图①，正方形ABCD中，E为对角线BD上一点，
过E点作EF⊥BD交BC于F，连接DF，G为DF中点，连接EG，CG．
（1）求证：EG=CG；
（2）将图①中△BEF绕B点逆时针旋转45º，如图②所示，取DF中点G，连接EG，CG．问（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由．
（3）将图①中△BEF绕B点旋转任意角度，如图③所示，再连接相应的线段，问（1）中的结论是否仍然成立？通过观察你还能得出什么结论？（均不要求证明）
为了打造重庆市“宜居城市”，某公园进行绿化改造，准备在公园内的一块四边形ABCD空地里栽一棵银杏树（如图），要求银杏树的位置点P到点A、D的距离相等，且到线段AD的距离等于线段a的长．请用尺规作图在所给图中作出栽种银杏树的位置点P．（要求不写已知、求作和作法，只需在原图上保留作图痕迹）．
如图，已知四边形ABCD是平行四边形，P、Q是对角线BD上的两个点，且AP∥QC．求证：BP=DQ．
如图，在△ABC中，AB=AC，D是底边BC的中点，作DE⊥AB于E，DF⊥AC于F
求证：DE=DF．
证明：∵AB=AC，∴∠B=∠C①．
在△BDE和△CDF中，∠B=∠C，∠BED=∠CFD，BD=CD，∴△BDE≌△CDF②．∴DE=DF③．
上面的证明过程是否正确？若正确，请写出①、②和③的推理根据．
（2）请你写出另一种证明此题的方法．
解方程：x﹣2=x（x﹣2）
如图，Rt△ABO的顶点A是双曲线y=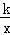
与直线y=﹣x﹣（k+1）在第二象限的交点．AB⊥x轴于B，且S△ABO=
．
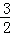（1）求这两个函数的解析式；
（2）求直线与双曲线的两个交点A、C的坐标和△AOC的面积．