（本小题满分13分）某沿海地区养殖的一种特色海鲜上市时间仅能持续5个月，预测上市初期和厢期会因供应不足使价格呈
持续上涨态势，而中期又将出现供大于求使价格连续下跌．现有三种价格模拟函数：①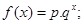
②
③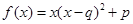
（以上三式中
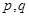均为常数，且q>l）．
（1）为准确研究其价格走势，应选哪种价格模拟函数（不必说明理由）；
（2）若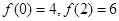
，求出所选函数
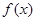的解析式（注：函数定义域是
．其中
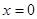表示8
月1日，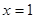
表示9月1日，…，以此类推）；
（3）在（2）的条件下研究下面课题：为保证养殖户的经济效益，当地政府计划在价格下跌期间积极拓宽外销，请你预测该海鲜将在哪几个月份内价格下跌．
（本小题满分12分）已知函数
（Ⅰ）求函数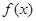
单调区间；
（Ⅱ）若
，求证：当
时，
．
（本小题满分12分）班主任为了对本班学生的考试成绩进行分析，决定从全班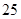
名女同学，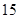
名男同学中随机抽取一个容量为
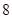的样本进行分析．随机抽出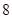位，他们的数学分数从小到大排序是：
、
、
、
、
、
、
、
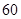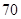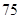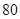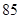，物理分数从小到大排序是：
、
、、
、
、、
、．
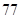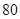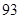（Ⅰ）若规定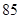分以上（包括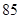分）为优秀，求这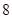位同学中恰有
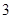位同学的数学和物理分数均为优秀的概率；
（Ⅱ）若这位同学的数学、物理分数对应如下表：
| 学生编号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 数学分数x |
60 |
65 |
70 |
75 |
80 |
85 |
90 |
95 |
| 物理分数y |
72 |
77 |
80 |
84 |
88 |
90 |
93 |
95 |
根据上表数据用变量
与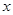
的相关系数或散点图说明物理成绩与数学成绩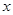之间是否具有线性相关性？如果具有线性相关性，求与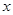的线性回归方程（系数精确到
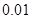）；如果不具有线性相关性，请说明理由．
参考公式：相关系数
；回归直线的方程是：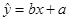
．
其中对应的回归估计值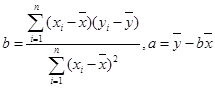
；
参考数据：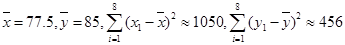
；
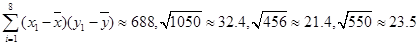
（本小题满分12分）某同学参加高校自主招生
门课程的考试．假设该同学第一门课程取得优秀成绩的概率为
，第二、第三门课程取得优秀成绩的概率分别为
，
，且不同课程是否取得优秀成绩相互独立．记
为该生取得优秀成绩的课程数，其分布列为
|
 |
 |
 |
|
|
 |
 |
 |
 |
（Ⅰ）求该生至少有门课程取得优秀成绩的概率及求，
的值；
（Ⅱ）求该生取得优秀成绩课程门数的数学期望
．
（本小题满分12分）
给出四个等式：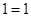
；
；
；
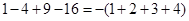
．猜测第
个等式，并用数学归纳法证明．
（本小题满分12分）已知函数
．
（Ⅰ）求曲线
在点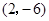
处的切线方程；
（Ⅱ）直线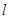
为曲线的切线，且经过原点，求直线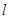的方程及切点坐标．