(本小题满分12分)班主任为了对本班学生的考试成绩进行分析,决定从全班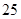 名女同学,
名女同学,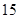 名男同学中随机抽取一个容量为
名男同学中随机抽取一个容量为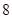 的样本进行分析.随机抽出
的样本进行分析.随机抽出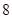 位,他们的数学分数从小到大排序是:
位,他们的数学分数从小到大排序是: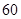 、
、 、
、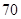 、
、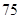 、
、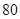 、
、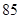 、
、 、
、 ,物理分数从小到大排序是:
,物理分数从小到大排序是: 、
、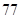 、
、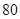 、
、 、
、 、
、 、
、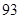 、
、 .
.
(Ⅰ)若规定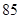 分以上(包括
分以上(包括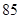 分)为优秀,求这
分)为优秀,求这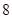 位同学中恰有
位同学中恰有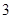 位同学的数学和物理分数均为优秀的概率;
位同学的数学和物理分数均为优秀的概率;
(Ⅱ)若这 位同学的数学、物理分数对应如下表:
位同学的数学、物理分数对应如下表:
| 学生编号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 数学分数x |
60 |
65 |
70 |
75 |
80 |
85 |
90 |
95 |
| 物理分数y |
72 |
77 |
80 |
84 |
88 |
90 |
93 |
95 |
根据上表数据用变量 与
与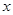 的相关系数或散点图说明物理成绩
的相关系数或散点图说明物理成绩 与数学成绩
与数学成绩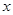 之间是否具有线性相关性?如果具有线性相关性,求
之间是否具有线性相关性?如果具有线性相关性,求 与
与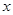 的线性回归方程(系数精确到
的线性回归方程(系数精确到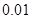 );如果不具有线性相关性,请说明理由.
);如果不具有线性相关性,请说明理由.
参考公式:相关系数 ;回归直线的方程是:
;回归直线的方程是: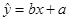 .
.
其中对应的回归估计值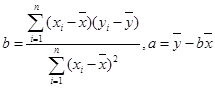 ;
;
参考数据: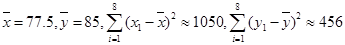 ;
;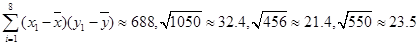
.(本小题满分12分)
如图4所示的茎叶图记录了甲、乙两个小组(每小组4人)在期末考试中
的数学成绩.乙组记录中有一个数据模糊,无法确认,在图中以 表示.
表示.
已知甲、乙两个小组的数学成绩的平均分相同.
(1)求 的值;
的值;
(2)求乙组四名同学数学成绩的方差;
(3)分别从甲、乙两组同学中各随机选取一名同学,记这两名同学数学
成绩之差的绝对值为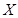 ,求随机变量
,求随机变量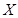 的分布列和均值(数学期望).
的分布列和均值(数学期望).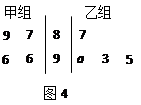
本小题满分12分)已知函数 .
.
(1)求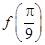 的值;
的值;
(2)设 ,若
,若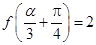 ,求
,求 的值.
的值.
已知函数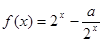 (
(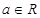 ),将
),将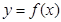 的图象向右平移两个单位,得到函数
的图象向右平移两个单位,得到函数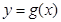 的图象,函数
的图象,函数 与函数
与函数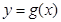 的图象关于直线
的图象关于直线 对称.
对称.
(1)求函数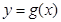 和
和 的解析式;
的解析式;
(2)若方程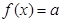 在
在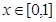 上有且仅有一个实根,求
上有且仅有一个实根,求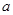 的取值范围;
的取值范围;
(3)设 ,已知
,已知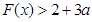 对任意的
对任意的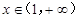 恒成立,求
恒成立,求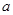 的取值范围.
的取值范围.
1已知函数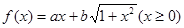 ,
,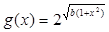 ,
,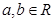 ,且
,且 ,
, .
.
(1)求 、
、 的解析式;
的解析式;
(2)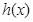 为定义在
为定义在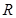 上的奇函数,且满足下列性质:①
上的奇函数,且满足下列性质:① 对一切实数
对一切实数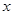 恒成立;②当
恒成立;②当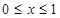 时
时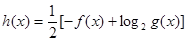 .
.
(ⅰ)求当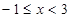 时,函数
时,函数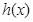 的解析式;
的解析式;
(ⅱ)求方程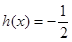 在区间
在区间 上的解的个数.
上的解的个数.
海水受日月的引力,在一定的时候发生涨落的现象叫潮,一般地,早潮叫潮,晚潮叫汐. 在通常情况下,船在涨潮时驶进航道,靠近码头;卸货后,在落潮时返回海洋. 下面是某港口在某季节每天的时间与水深关系表:
| 时刻 |
2:00 |
5:00 |
8:00 |
11:00 |
14:00 |
17:00 |
20:00 |
23:00 |
| 水深(米) |
7.5 |
5.0 |
2.5 |
5.0 |
7.5 |
5.0 |
2.5 |
5.0 |
经长期观测,这个港口的水深与时间的关系,可近似用函数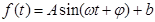
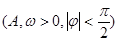 来描述.
来描述.
(1)根据以上数据,求出函数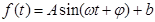 的表达式;
的表达式;
(2)一条货船的吃水深度(船底与水面的距离)为4.25米,安全条例规定至少要有2米的安全间隙(船底与洋底的距离),该船在一天内(0:00~24:00)何时能进入港口?在港口能停留多久?