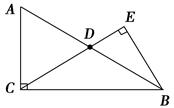
如图在Rt△ABC中,∠ACB=90°,D是边AB的中点,BE⊥CD,垂足为点E.已知AC=15,cos A= .
.
(1)求线段CD的长;
(2)求sin ∠DBE的值.
为配合我市创建省级文明城市,某校对八年级各班文明行为劝导志愿者人数进行了统计,各班统计人数有6名、5名、4名、3名、2名、1名共计六种情况,并制作如下两幅不完整的统计图.
(1)求该年级平均每班有多少文明行为劝导志愿者?并将条形图补充完整;
(2)该校决定本周开展主题实践活动,从八年级只有2名文明行为劝导志愿者的班级中任选两名,请用列表或画树状图的方法,求出所选文明行为劝导志愿者有两名来自同一班级的概率.
一不透明的布袋里,装有红、黄、蓝三种颜色的小球(除颜色外其余都相同),其中有红球2个,蓝球1个,黄球若干个,现从中任意摸出一个球是红球的概率为 .
.
(1)求口袋中黄球的个数;
(2)甲同学先随机摸出一个小球(不放回),再随机摸出一个小球,请用“树状图法”或“列表法”,求两次摸出都是红球的概率;
(3)现规定:摸到红球得5分,摸到黄球得3分,摸到蓝球得2分(每次摸后放回),乙同学在一次摸球游戏中,第一次随机摸到一个红球第二次又随机摸到一个蓝球,若随机再摸一次,求乙同学三次摸球所得分数之和不低于10分的概率.
我们可以用如下方法解不等式(x﹣1)(x+1)>0.
第一步:画出函数y=(x﹣1)(x+1)的图象;
第二步:找出图象与x轴的交点坐标,即交点坐标为(1,0),(﹣1,0);
第三步:根据图象可知,在x<﹣1或x>1时,y的值大于0.因此可得不等式(x﹣1)(x+1)>0的解集为x<﹣1或x>1.
请你仿照上述方法,求不等式x2﹣4<0的解集.
画图求方程x2=﹣x+2的解,你是如何解决的呢?我们来看一看下面两位同学不同的方法.
甲:先将方程x2=﹣x+2化为x2+x﹣2=0,再画出y=x2+x﹣2的图象,观察它与x轴的交点,得出方程的解;
乙:分别画出函数y=x2和y=﹣x+2的图象,观察它们的交点,并把交点的横坐标作为方程的解.
你对这两种解法有什么看法?请与你的同学交流.
如图是二次函数y=x2﹣2x﹣3的图象.
(1)求该抛物线的顶点坐标、与x轴的交点坐标
(2)观察图象直接指出x在什么范围内时,y>0?