如图，在平面直角坐标系中，抛物线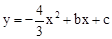
与x轴交于A、D两点，与y轴交于点B，四边形OBCD是矩形，点A的坐标为（1，0），点B的坐标为（0，4），已知点E（m，0）是线段DO上的动点，过点E作PE⊥x轴交抛物线于点P，交BC于点G，交BD于点H．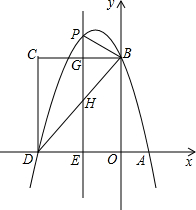
（1）求该抛物线的解析式；
（2）当点P在直线BC上方时，请用含m的代数式表示PG的长度；
（3）在（2）的条件下，是否存在这样的点P，使得以P、B、G为顶点的三角形与△DEH相似？若存在，求出此时m的值；若不存在，请说明理由．
在某市开展的“读中华经典，做书香少年”读书月活动中，围绕学生日人均阅读时间这一问题，对初二学生进行随机抽样调查．如图是根据调查结果绘制成的统计图（不完整），请你根据图中提供的信息解答下列问题：
（1）本次抽样调查的样本容量是多少？
（2）请将条形统计图补充完整．
（3）在扇形统计图中，计算出日人均阅读时间在1～1.5小时对应的圆心角度数．
（4）根据本次抽样调查，试估计该市12000名初二学生中日人均阅读时间在0.5～1.5小时的多少人．
如图，某校综合实践活动小组的同学欲测量公园内一棵树DE的高度，他们在这棵树
正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°，朝着这棵树的方向走到台阶下的点C处，测得树顶端D的仰角为60°.已知A点的高度AB为2米，台阶AC的坡度为1: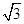
（即AB:AC＝1: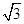），且B，C，E三点在同一条直线上．请根据以上条件求出树DE的高度（测倾器的高度忽见解析不计）．
先化简，再求值：
，其中x满足
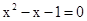
（1）计算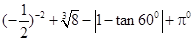
（2）解不等式组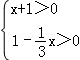
并把解集在数轴上表示出来．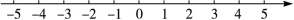
如图，抛物线y=－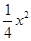
+
+4的图象与y轴交于点A，与x轴交于B、C两点，其对称轴与x轴交于点D，连接AC．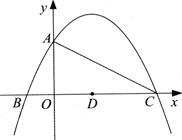
（1）点A的坐标为_______ ，点C的坐标为_______ ；
（2）线段AC上是否存在点E，使得△EDC为等腰三角形?若存在，求出所有符合条件的点E的坐标；若不存在，请说明理由；
（3）点P为x轴上方的抛物线上的一个动点，连接PA、PC，若所得△PAC的面积为S，则S取何值时，相应的点P有且只有2个?