如图，在平面直角坐标系
中，以
轴为始边作两个锐角
，它们的终边分别交单位圆于
两点．已知两点的横坐标分别是
，
．
（1）求
的值；
（2）求
的值．
(本小题满分12分)已知:如右图,在等腰梯形ABCD中,AD∥BC,AB＝DC,过点D作AC的平行线DE,交BA的延长线于点E．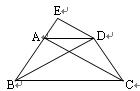
求证：（1）△ABC≌△DCB
（2）DE·DC＝AE·BD．
(本小题满分12分) 已知圆O1和O2交于A、B两点，AC为圆O1的切线，过B作两圆的割线DE交AC于P。
（1）求证：AD//EC
（2）若AD是圆O2的切线，且PA=6,PC=2,BD=9,求AD的长。
(本小题满分12分)在直角坐标系XOY中，以O为极点，X轴正半轴为极轴建立极坐标系。曲线C的极坐标方程是：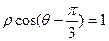
，M,N分别是曲线C与X、Y轴的交点。
（1）写出C的直角坐标系方程。并求M,N的极坐标。
（2）设MN的中点为P，求直线OP的极坐标方程。
(本题满分10)如图所示，已知AB为⊙O的直径，AC为弦，
，交AC于点D,BC=4cm,
（1）求OD的长；
（2）若
，求⊙O的直径.
某学校组织的一次篮球定点投篮训练中，规定每人最多投3次：在A处每投进一球得3分，在B处每投进一球得2分；如果前两次得分之和超过3分即停止投篮，否则投第三次。某学生在A处的命中率q1=0.25，在B处的命中率q2，该同学选择先在A处投一球，以后都在B处投，用X表示该同学投篮结束后所得的总分，其分布列如下：
| X |
0 |
2 |
3 |
4 |
5 |
| P |
0.03 |
p1 |
p2 |
p3 |
p4 |
（1）求q2的值；
（2）求随机变量X的均值E(X)；
（3）试比较该同学选择都在B处投篮得分超过3分与上述方式投篮得分超过3分的概率的大小。