(12分)抛物线的顶点在坐标原点,焦点在
轴的负半轴上,过点
作直线
与抛物线交于A,B两点,且满足
,
(1)求抛物线的方程
(2)当抛物线上的一动点P从A运动到B时,求
面积的的最大值．
已知函数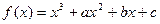
的图象过原点，且在x=1处取得极值，直线
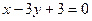与曲线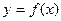
在原点处的切线互相垂直。
（I）求函数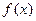
的解析式；
（II）若对任意实数的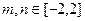
，恒有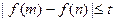
成立，求实数t的取值范围。
某医院用甲、乙两种药片为手术病人配营养餐，已知甲种药片每片含5单位的蛋白质和10单位的铁质，每片售价为3元；乙种药片每片含7单位的蛋白质和4单位的铁质，每片售价2元。若病人每餐
至少需要36单位的蛋白质和42单位的铁质，应使用甲、乙两种药片各几片才能既
满足营养要求又使费用最省？
已知A、B、C分别为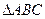
的三边a、b、c所对的角，向量
，
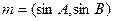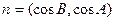，且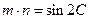
。
（1）求角C的大小；
（2）若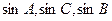
成等差
数列，且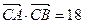
，求边c的长。
已知数列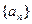
满足：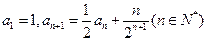
。
（I）已知数列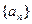的通项公式；
（II）证明：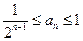
；
（III）设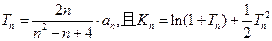
，证明：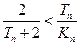
。
已知函数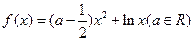
。
（I）当a=1时，求
在区间[1，e]的最大值和最小值；
（II）若在区间
上，函数的图象总在直线
的下方，求a的取值范围。