如图,四棱锥 的底面
的底面 为菱形,
为菱形, ,侧面
,侧面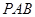 是边长为2的正三角形,侧面
是边长为2的正三角形,侧面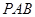
 底面
底面 .
.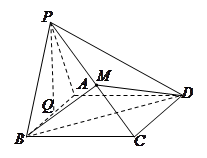
(Ⅰ)设 的中点为
的中点为 ,求证:
,求证: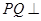 平面
平面 ;
;
(Ⅱ)求斜线 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(Ⅲ)在侧棱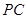 上存在一点
上存在一点 ,使得二面角
,使得二面角 的大小为
的大小为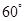 ,求
,求 的值.
的值.
【2015高考山东,理16】设 .
.
(Ⅰ)求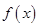 的单调区间;
的单调区间;
(Ⅱ)在锐角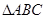 中,角
中,角 的对边分别为
的对边分别为 ,若
,若 ,求
,求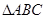 面积的最大值.
面积的最大值.
【2015高考浙江,理16】在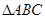 中,内角
中,内角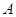 ,
,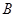 ,
,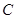 所对的边分别为
所对的边分别为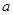 ,
,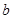 ,
,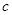 ,已知
,已知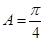 ,
,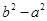 =
=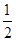
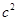 .
.
(1)求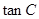 的值;
的值;
(2)若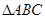 的面积为7,求
的面积为7,求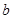 的值.
的值.
【2015高考福建,理19】已知函数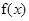 的图像是由函数
的图像是由函数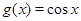 的图像经如下变换得到:先将
的图像经如下变换得到:先将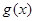 图像上所有点的纵坐标伸长到原来的2倍(横坐标不变),再将所得到的图像向右平移
图像上所有点的纵坐标伸长到原来的2倍(横坐标不变),再将所得到的图像向右平移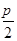 个单位长度.
个单位长度.
(Ⅰ)求函数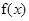 的解析式,并求其图像的对称轴方程;
的解析式,并求其图像的对称轴方程;
(Ⅱ)已知关于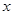 的方程
的方程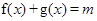 在
在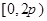 内有两个不同的解
内有两个不同的解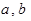 .
.
(1)求实数m的取值范围;
(2)证明: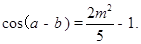
【2015江苏高考,15】(本小题满分14分)在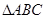 中,已知
中,已知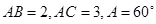 .
.
(1)求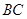 的长;
的长;
(2)求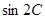 的值.
的值.
【2015高考新课标2,理17】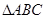 中,
中,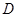 是
是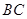 上的点,
上的点,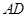 平分
平分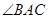 ,
,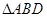 面积是
面积是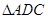 面积的2倍.
面积的2倍.
(Ⅰ)求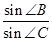 ;
;
(Ⅱ)若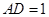 ,
,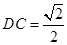 ,求
,求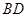 和
和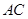 的长.
的长.