(本小题满分10分)【选修4—1:几何证明选讲】
在直角坐标系中,以原点为极点, 轴的正半轴为极轴建坐标系,已知曲线
轴的正半轴为极轴建坐标系,已知曲线
 ,已知过点
,已知过点 的直线
的直线 的参数方程为
的参数方程为 (
( 为参数),直线
为参数),直线 与曲线
与曲线 分别交于
分别交于 两点。
两点。
(1)写出曲线 和直线
和直线 的普通方程;
的普通方程;
(2)若 成等比数列,求
成等比数列,求 的值.
的值.
(本小题满分14分)
如图,直线 与椭圆
与椭圆 交于
交于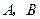 两点,记
两点,记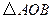 的面积为
的面积为 .
.
(I)求在 ,
, 的条件下,
的条件下, 的最大值;
的最大值;
(II)当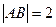 ,
,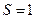 时,求直线
时,求直线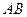 的方程.
的方程.
(本小题满分14分)某商店经销一种广州亚运会纪念品,每件产品成本为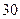 元,且每卖出一件产品,需向税务部门上交
元,且每卖出一件产品,需向税务部门上交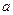 元(
元(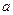 为常数,
为常数,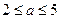 )的税收,设每件产品的日售价为
)的税收,设每件产品的日售价为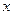 元(
元( ),根据市场调查,日销售量与
),根据市场调查,日销售量与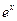 (
(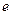 为自然对数的底数)成反比,已知每件产品的日售价为
为自然对数的底数)成反比,已知每件产品的日售价为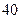 元,日销售量为
元,日销售量为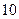 件。w.w.w..c.o.m
件。w.w.w..c.o.m
(1)求商店的日利润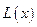 元与每件产品的日售价
元与每件产品的日售价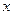 元的函数关系式;
元的函数关系式;
(2)当每件产品的日售价为多少时该商店的日利润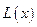 最大,说明理由.
最大,说明理由.
(本小题满分14分)直棱柱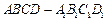 中,底面
中,底面 是直角梯形,
是直角梯形,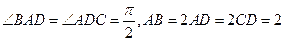
(Ⅰ)求证: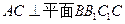
(Ⅱ)在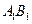 上是否存一点
上是否存一点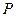 ,使得
,使得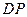 与平面
与平面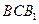 与平面
与平面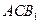 都平行?证明你的结论.
都平行?证明你的结论.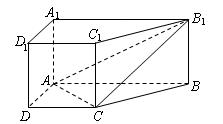
(本小题满分12分)
随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图所示。
(1)根据茎叶图判断哪个班的平均身高较高; (2)现从乙班这10名同学中随机抽取两
(2)现从乙班这10名同学中随机抽取两 名身高不低于
名身高不低于
173cm的同学,求身高为176cm的同学被抽中的概率。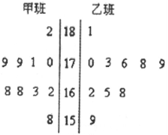
已知函数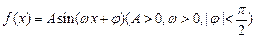 的部分图象如图所示.(Ⅰ)求函数
的部分图象如图所示.(Ⅰ)求函数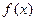 的解析式;
的解析式;
(Ⅱ)如何由函数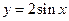 的图象通过适当的
的图象通过适当的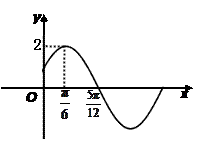 变换得到函数
变换得到函数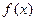 的图象, 写出变换过程.
的图象, 写出变换过程.