（本小题满分12分）
随机抽取某中学甲、乙两班各10名同学，测量他们的身高（单位：cm），获得身高数据的茎叶图如图所示。
（1）根据茎叶图判断哪个班的平均身高较高；
（2）现从乙班这10名同学中随机抽取两
名身高不低于
173cm的同学，求身高为176cm的同学被抽中的概率。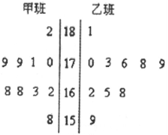
已知数列
的各项均为正整数，对于任意n∈N*，都有
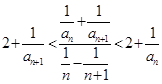成立，且
．
（1）求
，
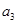的值；
（2）猜想数列的通项公式，并给出证明．
（本小题满分10分）如图，在直三棱柱
中，已知
，
，
，点
，
分别在棱
，
上，且
，
，
． 
（1）当
时，求异面直线
与
所成角的大小；
（2）当直线
与平面
所成角的正弦值为
时，求
的值．
在平面直角坐标系
中，已知曲线
的参数方程是
（
是参数），若以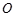
为极点，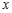
轴的正半轴为极轴，取与直角坐标系中相同的单位长度，建立极坐标系，求曲线的极坐标方程．
已知二阶矩阵A有特征值
及对应的一个特征向量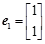
和特征值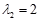
及对应的一个特征向量
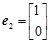，试求矩阵A．
已知数列
是等差数列，其前n项和为Sn，若
，
．
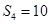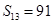（1）求
；
（2）若数列{Mn}满足条件： 
，当
时，
－
，其中数列
单调递增，且
，
．
①试找出一组
，
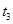，使得
；
②证明：对于数列，一定存在数列，使得数列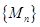
中的各数均为一个整数的平方．