已知圆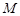 的方程为
的方程为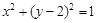 ,直线
,直线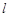 的方程为
的方程为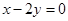 ,点
,点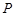 在直线
在直线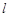 上,过
上,过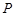 点作圆
点作圆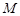 的切线
的切线 ,切点为
,切点为 .
.
(1)若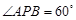 ,试求点
,试求点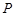 的坐标;
的坐标;
(2)求证:经过 三点的圆必过定点,并求出所有定点的坐标;
三点的圆必过定点,并求出所有定点的坐标;
(3)求弦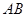 长的最小值.
长的最小值.
有一种大型商品,A、B两地都有出售,且价格相同,某地居民从两地之一购得商品后运回的费用是:A地每公里的运费是B地每公里运费的3倍. A、B两地距离为10公里,顾客选择A地或B地购买这件商品的标准是:包括运费和价格的总费用较低.已知P地居民选择A地或B地购物总费用相等.
(1)以A、B所在的直线为x轴,线段AB的中点为原点建立如图直角坐标系,试确定点P所在曲线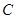 的形状;
的形状;
(2)请说明(1)中曲线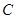 外的居民选择A地购物是否合算?
外的居民选择A地购物是否合算?
已知数列{ }满足对所有的
}满足对所有的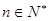 都有
都有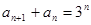 成立,且
成立,且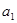 =1.
=1.
①求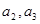 的值;
的值;
②求数列 的通项公式;
的通项公式;
③令 ,数列{
,数列{ }的前
}的前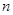 项和为
项和为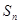 ,试比较
,试比较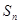 与
与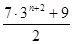 的大小关系.
的大小关系.
已知数列 满足
满足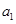 =1,且
=1,且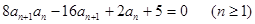
记 
(Ⅰ)求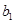 、
、 、
、 的值;
的值;
(Ⅱ) 求数列 的通项公式;
的通项公式;
(Ⅲ)求数列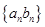 的前
的前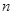 项和
项和 .
.
已知数列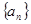 的前
的前 项和是
项和是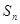 ,满足
,满足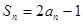 .
.
(Ⅰ)求数列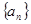 的通项
的通项 及前
及前 项和
项和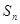 ;
;
(Ⅱ)若数列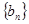 满足
满足 ,求数列
,求数列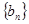 的前
的前 项和
项和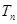 ;
;
(Ⅲ)若对任意的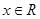 ,恒有
,恒有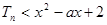 成立,求实数
成立,求实数 的取值范围
的取值范围