如图,在平面直角坐标系 中,已知椭圆
中,已知椭圆 :
: ,设
,设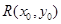 是椭圆
是椭圆 上的任一点,从原点
上的任一点,从原点 向圆
向圆 :
: 作两条切线,分别交椭圆于点
作两条切线,分别交椭圆于点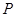 ,
,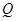 .
.
(1)若直线 ,
, 互相垂直,求圆
互相垂直,求圆 的方程;
的方程;
(2)若直线 ,
, 的斜率存在,并记为
的斜率存在,并记为 ,
,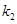 ,求证:
,求证: ;
;
(3)试问 是否为定值?若是,求出该值;若不是,说明理由.
是否为定值?若是,求出该值;若不是,说明理由.
某电视台连续播放6个广告,其中有3个不同的商业广告、两个不同的世博会宣传广告、一个公益广告,要求最后播放的不能是商业广告,且世博会宣传广告与公益广告不能连续播放,两个世博会宣传广告也不能连续播放,则有多少种不同的播放方式?
将红、黄、绿、黑四种不同的颜色涂入如图中的五个区域内,要求相邻的两个区域的颜色都不相同,则有多少种不同的涂色方法?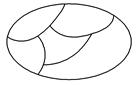
某班一天上午有4节课,每节都需要安排一名教师去上课,现从A,B,C,D,E,F,6名教师中安排4人分别上一节课,第一节课只能从A、B两人中安排一人,第四节课只能从A、C两人中安排一人,则不同的安排方案共有多少种?
某班新年联欢晚会原定的5个节目已排成节目单,开演前又增加了两个新节目,如果将这2个节目插入原节目单中,那么有多少种不同的插法?
甲、乙、丙3位志愿者安排在周一至周五的5天中参加某项志愿者活动,要求每人参加一天且每天至多安排一人,并要求甲安排在另外两位前面,不同的安排方法共有多少种?