(本小题满分13分)已知函数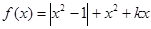 .
.
(1)若对于区间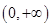 内的任意
内的任意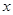 ,总有
,总有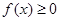 成立,求实数
成立,求实数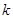 的取值范围;
的取值范围;
(2)若函数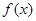 在区间
在区间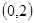 内有两个不同的零点
内有两个不同的零点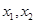 ,求:
,求:
①实数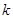 的取值范围; ②
的取值范围; ② 的取值范围.
的取值范围.
(本小题满分12分)已知函数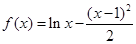 .
.
(Ⅰ)求函数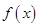 的单调递增区间;
的单调递增区间;
(Ⅱ)证明:当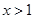 时,
时, .
.
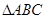 中,
中,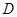 是
是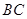 上的点,
上的点,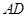 平分
平分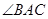 ,
,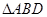 面积是
面积是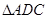 面积的2倍.
面积的2倍.
(Ⅰ) 求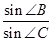 ;
;
(Ⅱ)若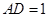 ,
,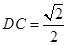 ,求
,求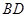 和
和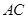 的长.
的长.
(本小题12分)已知向量 ,
, ,函数
,函数
(Ⅰ)求函数 的单调递增区间;
的单调递增区间;
(Ⅱ)在 中,内角
中,内角 的对边分别为
的对边分别为 ,且
,且 ,若对任意满足条件的
,若对任意满足条件的 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题满分11分)已知数列 的前
的前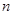 项和
项和 .
.
(1)求数列 的通项公式;
的通项公式;
(2)证明:对任意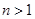 ,都有
,都有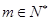 ,使得
,使得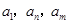 成等比数列.
成等比数列.
(本小题满分12分)已知椭圆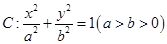 ,其中
,其中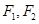 为左、右焦点,且离心率
为左、右焦点,且离心率 ,直线
,直线 与椭圆交于两不同点
与椭圆交于两不同点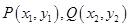 .当直线
.当直线 过椭圆C右焦点F2且倾斜角为
过椭圆C右焦点F2且倾斜角为 时,原点O到直线
时,原点O到直线 的距离为
的距离为 .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若 ,当
,当 面积为
面积为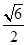 时,求
时,求 的最大值.
的最大值.