如图,侧棱垂直底面的三棱柱 中,
中,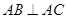 ,
, ,
,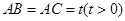 ,
,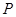 是侧棱
是侧棱 上的动点.
上的动点.
(1)当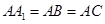 时,求证:
时,求证: ;
;
(2)若二面角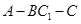 的平面角的余弦值为
的平面角的余弦值为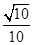 ,试求实数
,试求实数 的值.
的值.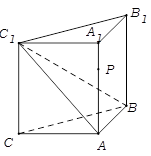
已知两个集合 ,
,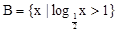 ;命题p:实数m为小于6的正实数,命题q:A是B成立的必要不充分条件,若命题
;命题p:实数m为小于6的正实数,命题q:A是B成立的必要不充分条件,若命题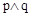 是真命题,求实数m的值.
是真命题,求实数m的值.
若a,b,c均为实数,且 ,
,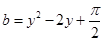 ,
, ,
,
试用反证法证明:a,b,c中至少有一个大于0.
设 是由满足下列条件的函数
是由满足下列条件的函数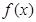 构成的集合:“①函数
构成的集合:“①函数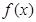 的导数
的导数 满足
满足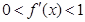 ;②方程
;②方程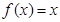 有实数根”.
有实数根”.
(I)判断函数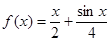 是否是集合
是否是集合 中的元素,并说明理由;
中的元素,并说明理由;
(II)集合 中的元素
中的元素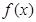 具有下面的性质:若
具有下面的性质:若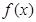 的定义域为D,则对于任意
的定义域为D,则对于任意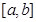
 D,都存在
D,都存在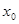

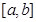 ,使得等式
,使得等式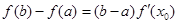 成立”,试用这一性质证明:方程
成立”,试用这一性质证明:方程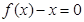 只有一个实数根;
只有一个实数根;
(III)设 是方程
是方程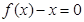 的实数根,求证:对于
的实数根,求证:对于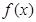 定义域中任意的
定义域中任意的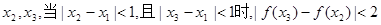 .
.
已知函数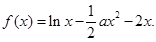
(I)若 ,求
,求 的增区间;
的增区间;
(II)若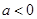 ,且函数
,且函数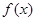 存在单调递减区间,求
存在单调递减区间,求 的取值范围;
的取值范围;
(III)若 且关于
且关于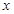 的方程
的方程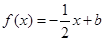 在
在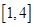 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数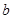 的取值范围.
的取值范围.