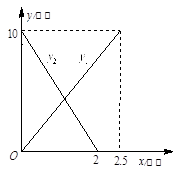某中学八年级(5)班的学生到野外进行数学活动,为了测量一池塘两端A、B之间的距离,同学们设计了如下两种方案:
(Ⅰ)如图3(1),先在平地上取一个可以直接到达A、B的点C,再连接AC、BC,并分别延长AC至D,BC至E,使 ,
,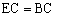 ,最后量出DE的距离就是AB的长。
,最后量出DE的距离就是AB的长。
(Ⅱ)如图3(2),过点B作AB的垂线BF,在BF上取C、D两点,使BC=CD,接着过D作BD的垂线DE,交AC的延长线于E,则测出DE的长即为AB的距离。
问:(1)方案(Ⅰ)是否可行?__________ _;
(2)方案(Ⅱ)是否可行?___________;
(3)小明说在方案(Ⅱ)中,并不一定须要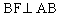 ,DE⊥BF,只需___________就可以了,请把小明所说的条件补上,并写出证明过程。
,DE⊥BF,只需___________就可以了,请把小明所说的条件补上,并写出证明过程。
证明: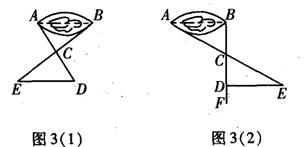
已知:二次函数的图象经过原点,对称轴是直线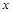 =-2,最高点的纵坐标为4,
=-2,最高点的纵坐标为4,
求:该二次函数解析式。
计算: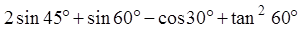
如图1,在直角梯形ABCD中,AD//BC,∠A=90°,AB=8cm,AD=6cm, BC=10cm。点P从点B出发沿BD方向匀速运动,速度为1cm/s;同时,线段EF从CD出发沿DA方向匀速运动,速度为1 cm/s,且EF与BD交于点Q,连接PE、PF。当点P与点Q相遇时,所有运动停止。若设运动时间为t(s).
(1)求CD的长度
(2)当PE//AB时,求t的值;
(3)①设△PEF的面积为S,求S关于t的函数关系式;
②如图2,当△PEF的外接圆圆心O恰好在EF中点时,则t的值为(请直接写出答案)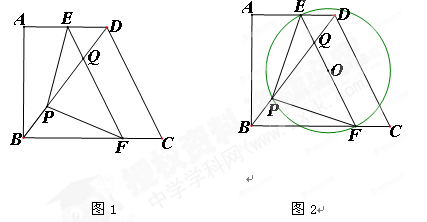
已知:以原点O为圆心,5为半径的半圆与y轴交于A、G两点,AB与半圆相切于点A,点B的坐标为(3,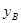 )。(如图1
)。(如图1 )过半圆上的点C
)过半圆上的点C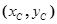 作y轴的垂线,垂足为D.Rt△DOC的面积为
作y轴的垂线,垂足为D.Rt△DOC的面积为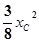 。
。
(1)求点C的坐标;
(2)①命题“如图2,以y轴为对称轴的等腰梯形MNPQ与M1N1P1Q1的上底和下底都分别在同一条直线上,NP∥MQ,PQ∥P1Q1,且NP>MQ.设抛物线y=a0x2+h0过点P、Q,抛物线y=a1x2+h1过点P1、Q1,则h0>h1”是真命题.请你以Q(3,5)、P(4,3)和Q1(p,5)、P1(p+1,3)为例进行验证;
②当图1中的线段BC在第一象限时,作线段BC关于y轴对称的线段FE,连接BF、CE,点T是线段BF上的动点(如图3);设K是过T、B、C三点的抛物线y=ax2+bx+c的顶点,求K的纵坐标yK的取值范围.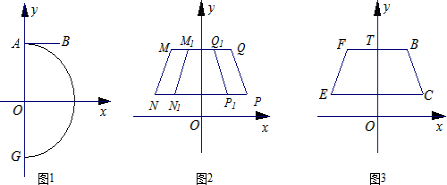
某中学九年级甲、乙两班商定举行一次远足活动,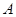 、
、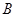 两地相距10千米,甲班从
两地相距10千米,甲班从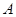 地出发匀速步行到
地出发匀速步行到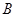 地,乙班从
地,乙班从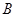 地出发匀速步行到
地出发匀速步行到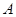 地.两班同时出发,相向而行.设步行时间为
地.两班同时出发,相向而行.设步行时间为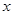 小时,甲、乙两班离
小时,甲、乙两班离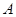 地的距离分别为
地的距离分别为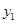 千米、
千米、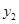 千米,
千米,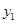 、
、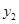 与
与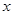 的函数关系图象如图所示,根据图象解答下列问题:
的函数关系图象如图所示,根据图象解答下列问题:
(1)直接写出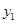 、
、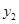 与
与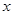 的函数关系式;
的函数关系式;
(2)求甲、乙两班学生出发后,几小时相遇?相遇时乙班离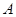 地多少千米?
地多少千米?
(3)甲、乙两班相距4千米时所用时间是多少小时?