在数学课的学习中,我们已经接触了很多代数恒等式,知道可以用图形的面积来解释这些代数恒等式.如图①可以解释恒等式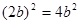 ;
; 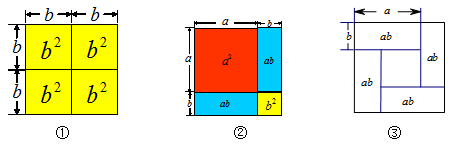
(1)如图②可以解释恒等式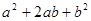 = .
= .
(2)如图③是由4个长为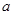 ,宽为
,宽为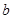 的长方形纸片围成的正方形,
的长方形纸片围成的正方形,
①用面积关系写出一个代数恒等式: .
②若长方形纸片的面积为3,且长比宽长3,求长方形的周长(其中a.b都是正数,结果可保留根号)
(共8分)已知多项式 ,计算
,计算 .某同学做此题时误将
.某同学做此题时误将 看成了
看成了 ,求得其结果为
,求得其结果为 =
= ,若
,若 ,请你帮助他求得正确答案.
,请你帮助他求得正确答案.
(共10分)有理数 、
、 在数轴上对应点如图所示:
在数轴上对应点如图所示:
(1)在数轴上表示
 、|y|;
、|y|;(2)试把
 、
、 、0、
、0、 、︱y︱这五个数从小到大用“<”号连接起来.
、︱y︱这五个数从小到大用“<”号连接起来.(3)化简|x+y|-|y-x|﹢|y|
解方程 (每小题5分,共10分)(1)

(2)

计算:(前3题每小题4分,第(4)题6分,共18分)(1)

(2)
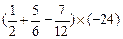
(3)
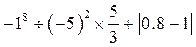
(4)先化简,再求值。
 ;其中a=—2,b=3
;其中a=—2,b=3
应用题。1、某厂一车间上半年生产零件48万件,是下半年产量的
 ,该车间全年的产量是多少?
,该车间全年的产量是多少?2、高铁列车的运行速度是380千米/小时,普通列车的速度是它的
 。普通列车的速度是多少?
。普通列车的速度是多少?3、用120cm的铁丝做一个长方体框架。长、宽、高的比是3:2:1。这个长方体的体积是多少?
4、一个圆形花坛。周长是25.12m。如果在这个花坛的周围铺上一条宽1m的环形小路,这条小路的面积是多少平方米?
5、校园里有杨树40棵,是柳树的
 。松树棵数是柳树的
。松树棵数是柳树的 。松树有多少棵?
。松树有多少棵?6、某厂为青海玉树灾区赶制一批帐篷。第一天生产了这批帐篷的
 ,第二天生产了总数的
,第二天生产了总数的 。两天共生产4400顶。第一天生产了多少顶?
。两天共生产4400顶。第一天生产了多少顶?