如图所示，已知倾角为θ=45°、高为h的斜面固定在水平地面上．一小球从高为H（h＜H＜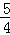
h）处自由下落，与斜面做无能量损失的碰撞后水平抛出．小球自由下落的落点距斜面左侧的水平距离x满足一定条件时，小球能直接落到水平地面上．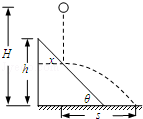
（1）求小球落到地面上的速度大小；
（2）求要使小球做平抛运动后能直接落到水平地面上，x应满足的条件；
（3）在满足（2）的条件下，求小球运动的最长时间．
如图所示，小球A系在细线的一端，线的另一端固定在O点，O点到水平面的距离为h。物块B质量是小球的5倍，置于粗糙的水平面上且位于O点的正下方，物块与水平面间的动摩擦因数为μ。现拉动小球使线水平伸直，小球
由静止开始释放，运动到最低点时与物块发生正碰（碰撞时间极短），反弹后上升至最高点时到水平面的距离为h/16。小球与物块均视为质点，不计空气阻力，重力加速度为g，求物块在水平面上滑行的时间t。
两根足够长的固定的平行金属导轨位于同一水平面内，两导轨间的距离为L。导轨上面横放着两根导体棒ab和cd，构成矩形回路，如图所示．两根导体棒的质量皆为m，电阻皆为R，回路中其余部分的电阻可不计．在整个导轨平面内都有竖直向上的匀强磁场，磁感应强度为B．设两导体棒均可沿导轨无摩擦地滑行．开始时，棒cd静止，棒ab有指向棒cd的初速度v0．若两导体棒在运动中始终不接触，求：
（1）在运动中产生的焦耳热最多是多少．
（2）当ab棒的速度变为初速度的3/4时，cd棒的加速度是多少？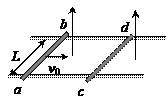
如图13所示，竖直向上的匀强磁场，开始时磁感应强度B="0.5" T，并且以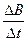
="0.1" T/s在变化，水平轨道电阻不计，且不计摩擦阻力，宽0.5 m的导轨上放一电阻R0="0.1" Ω的导体棒，并用水平线通过定滑轮吊着质量M="0.2" kg的重物，轨道左端连接的电阻R="0.4" Ω，图中的l="0.8" m，求至少经过多长时间才能吊起重物.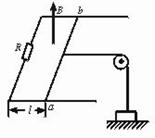
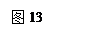
如图12所示，空间分布着有理想边界的匀强电场和匀强磁场。左侧匀强电场的场强大小为E、方向水平向右，电场宽度为L；中间区域匀强磁场的磁感应强度大小为B，方向垂直纸面向里。一个质量为m、电量为q、不计重力的带正电的粒子从电场
的左边缘的O点由静止开始运动，穿过中间磁场区域进入右侧磁场区域后，又回到O点，然后重复上述运动过程。求：
（1）中间磁场区域的宽度d；
（2）带电粒子从O点开
始运动到第一次回到O点所用时间t.
发电机输出功率为100 kW，输出电压是250 V，用户需要的电压是220 V，输电线电阻为10 Ω.若输电线中因发热而损失的功率为输送功率的4%，试求：
（1）在输电线路中设置的升、降压变压器原副线圈的匝数比.
（2）画出此输电线路的示意图
.
（3）用户得到的电功率是多少？