如图所示,质量为m的小物块放在长直水平面上,用水平细线紧绕在半径为R、质量为2m的薄壁圆筒上.t=0时刻,圆筒在电动机带动下由静止开始绕竖直中心轴转动,转动中角速度满足ω=βt(β为已知常数),物块和地面之间动摩擦因数为μ.求: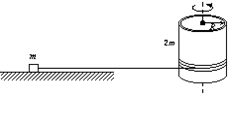
(1)物块运动中受到的拉力.(2)从开始运动至t=t1时刻,电动机对物块做了多少功?
如图所示,人重300N,物体重200N,地面粗糙,当人用100N的力向下拉绳子时,人和物体均处于静止状态,绳子与水平方向夹角为30°。求:
(1)人对地面的压力的大小与方向。
(2) 物体对地面的压力的大小与方向.
如图所示,一儿童玩具静止在水平地面上,一个幼儿沿与水平面成53°角的恒力拉着它沿水平面运动,已知拉力F=4.0N,玩具的质量m=0.5kg,经过时间t=2.0s,玩具移动了距离x=4.8m,这时幼儿松开手,玩具又滑行了一段距离后停下.
(1)全过程玩具的最大速度是多大?(2)松开手后玩具还能运动多远?
(取g=10m/s2.sin53°=0.8,cos53°=0.6)
2010年11月23日,朝韩突然互射炮弹,5天之后韩国与美国在西部海域举行联合军事演习,美国“乔治·华盛顿”号航空母舰将参加.演习过程中美国航母与一艘韩国舰艇在同一条直线上同向航行,某时刻韩国舰艇在美国航母前面8 km处,速度大小为20 m/s,从该时刻起由于发动机故障而以0.2 m/s2的加速度匀减速运动,美国航母一直以40 m/s的速度匀速航行,求:从韩国舰艇发生故障开始,经过多长时间美国航母追上韩国舰艇?
一个物体的初速度是2m/s,以0.5m/s2的加速度做匀加速直线运动,求:
(1)物体在第3秒末的速度;
(2)物体在头4秒内的位移;
(3)物体在第5秒内的位移。
如下图所示,在水平粗糙横杆上,有一质量为m的小圆环A,用一细线悬吊一个质量为m的球B。现用一水平拉力缓慢地拉起球B,使细线与竖直方向成37°角,此时环A仍保持静止(sin37°=0.6,cos37°=0.8),求: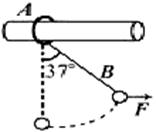
(1)此时水平拉力F的大小;
(2)环对横杆的压力及环受到的摩擦力。