(本小题满分14分)已知函数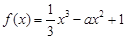 .
.
(Ⅰ)若函数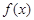 的图象关于点
的图象关于点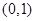 对称,直接写出
对称,直接写出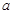 的值;
的值;
(Ⅱ)求函数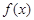 的单调递减区间;
的单调递减区间;
(Ⅲ)若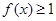 在区间
在区间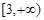 上恒成立,求
上恒成立,求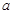 的最大值.
的最大值.
已知在正四棱锥 -
- 中(如图),高为1
中(如图),高为1  ,其体积为4
,其体积为4  ,求异面直线
,求异面直线 与
与 所成角的大小.
所成角的大小.
本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分.
已知数列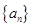 满足
满足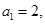 前
前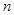 项和为
项和为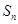 ,
,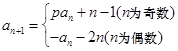 .
.
(1)若数列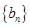 满足
满足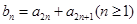 ,试求数列
,试求数列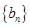 前3项的和
前3项的和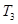 ;
;
(2)(理)若数列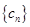 满足
满足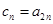 ,试判断
,试判断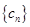 是否为等比数列,并说明理由;
是否为等比数列,并说明理由;
(文)若数列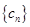 满足
满足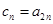 ,
,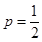 ,求证:
,求证: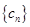 是为等比数列;
是为等比数列;
(3)当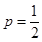 时,对任意
时,对任意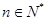 ,不等式
,不等式 都成立,求
都成立,求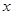 的取值范围.
的取值范围.
(本题满分16分)本题共有3个小题,第1小题满分5分,第2小题满分6分,第3小题满分5分.
已知函数 是奇函数,定义域为区间D(使表达式有意义的实数x 的集合).
是奇函数,定义域为区间D(使表达式有意义的实数x 的集合).
(1)求实数m的值,并写出区间D;
(2)若底数 ,试判断函数
,试判断函数 在定义域D内的单调性,并证明;
在定义域D内的单调性,并证明;
(3)当 (
( ,a是底数)时,函数值组成的集合为
,a是底数)时,函数值组成的集合为 ,求实数
,求实数 的值.
的值.
本题共有2个小题,第1小题满分6分,第2小题满分8分.
如图1, ,
, 是某地一个湖泊的两条互相垂直的湖堤,线段
是某地一个湖泊的两条互相垂直的湖堤,线段 和曲线段
和曲线段 分别是湖泊中的一座栈桥和一条防波堤。为观光旅游的需要,拟过栈桥
分别是湖泊中的一座栈桥和一条防波堤。为观光旅游的需要,拟过栈桥 上某点
上某点 分别修建与
分别修建与 ,
, 平行的栈桥
平行的栈桥 、
、 ,且以
,且以 、
、 为边建一个跨越水面的三角形观光平台
为边建一个跨越水面的三角形观光平台 。建立如图2所示的直角坐标系,测得线段
。建立如图2所示的直角坐标系,测得线段 的方程是
的方程是 ,曲线段
,曲线段 的方程是
的方程是 ,设点
,设点 的坐标为
的坐标为 ,记
,记 。(题中所涉及的长度单位均为米,栈桥和防波堤都不计宽度)
。(题中所涉及的长度单位均为米,栈桥和防波堤都不计宽度)
(1)求 的取值范围;
的取值范围;
(2)试写出三角形观光平台 面积
面积 关于
关于 的函数解析式,并求出该面积的最小值
的函数解析式,并求出该面积的最小值
(本题满分12分) 本题共有2个小题,第1小题满分5分,第2小题满分7分.
已知函数 ,数列
,数列 满足
满足  ,
, .
.
(1)若数列 是常数列,求a的值;
是常数列,求a的值;
(2)当 时,记
时,记 ,证明数列
,证明数列 是等比数列,并求
是等比数列,并求 .
.