(本小题满分12分)
某学校高一年级为了了解学生在一次数学考试中的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分是100分)作为样本(样本容量为a)进行统计,按照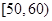 ,
, ,
,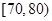 ,
, ,
,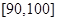 的分组作出如图甲所示的频率分布直方图和图乙所示的样本分数的茎叶图(图乙中仅列出了得分在
的分组作出如图甲所示的频率分布直方图和图乙所示的样本分数的茎叶图(图乙中仅列出了得分在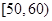 ,
,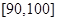 的数据).
的数据).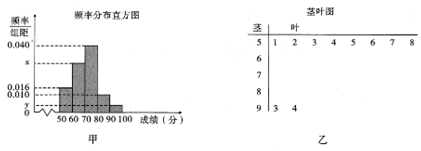
(Ⅰ)求样本容量n和频率分布直方图中x,y的值;
(Ⅱ)在选取的样本中,从考试成绩是80分以上(含80分)的同学中随机抽取3名同学为其他同学作交流,设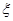 表示所抽取的3名同学中得分在
表示所抽取的3名同学中得分在 的学生个数,求
的学生个数,求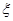 的分布列及其数学期望.
的分布列及其数学期望.
已知函数
(1)求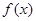 的解析式及减区间;
的解析式及减区间;
(2)若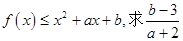 的最小值。
的最小值。
已知椭圆C的方程为 左、右焦点分别为F1、F2,焦距为4,点M是椭圆C上一点,满足
左、右焦点分别为F1、F2,焦距为4,点M是椭圆C上一点,满足
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点P(0,2)分别作直线PA,PB交椭圆C于A,B两点,设直线PA,PB的斜率分别为k1,k2, ,求证:直线AB过定点,并求出直线AB的斜率k的取值范围。
,求证:直线AB过定点,并求出直线AB的斜率k的取值范围。
如图。在直三棱柱ABC—A1B1C1中,AB=BC=2AA1,∠ABC=90°,M是BC中点。
(I)求证:A1B∥平面AMC1;
(II)求直线CC1与平面AMC1所成角的正弦值;
(Ⅲ)试问:在棱A1B1上是否存在点N,使AN与MC1成角60°?若存在,确定点N的位置;若不存在,请说明理由。
某校从参加某次知识竞赛的同学中,选取60名同学将其成绩(百分制,均为整数)分成6组后,得到部分频率分布直方图(如图),观察图中的信息,回答下列问题.
(Ⅰ)求分数在[70,80)内的频率,并补全这个频率分布直方图;
(Ⅱ)根据频率分布直方图,估计本次考试的平均分;
(Ⅲ)若从60名学生中随机抽取2人,抽到的学生成绩在[40,70)记0分,记[70,100]记1分,用X表示抽取结束后的总记分,求X的分布列和数学期望。
已知数列{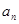 }中
}中
(I)设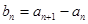 ,求证数列{
,求证数列{ }是等比数列;
}是等比数列;
(Ⅱ)求数列{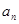 }的通项公式.
}的通项公式.