（本小题满分12分）
据调查统计，通过这两条公路从城市甲到城市乙的200辆汽车所用时间的频数如下表：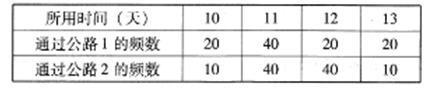
（Ⅰ）为进行某项研究，从所用时间为12天的60辆汽车中随机抽取6辆.
（ⅰ）若用分层抽样的方法抽取，求从通过公路1和公路2的汽车中各抽取几辆？
（ⅱ）若从（ⅰ）的条件下抽取的6辆汽车中，再任意抽取两辆汽车，求这两辆汽车至少有一辆通过公路1的概率？
（Ⅱ）假设汽车A只能在约定日期（某月某日）的前11天出发，汽车B只能在约定日期的前12天出发.为了尽最大可能在各自允许的时间内将货物运往城市乙，估计汽车A和汽车B应如何选择各自的路径？
已知函数f(x)=x2+2ax-3:
(1)如果f(a+1)-f(a)=9,求a的值；（2）问a为何值时，函数的最小值是-4。
一个盒子中装有4张卡片，每张卡片上写有1个数字，数字分别是1、2、3、4。现从盒子中随机抽取卡片．
(I)若一次抽取3张卡片，求3张卡片上数字之和大于7的概率；
(II)若第一次抽1张卡片，放回后再抽取1张卡片，求两次抽取中至少一次抽到数字3的概率．
已知
(Ⅰ)若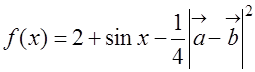
,求
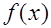的表达式；
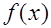（Ⅱ）若函数和函数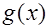
的图象关于原点对称，求函数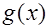的解析式；
（Ⅲ）若
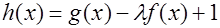在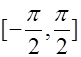
上是增函数，求实数
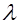的取值范围.
函数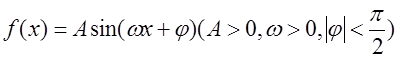
的部分图象如图所示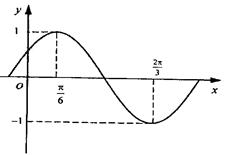
(1)求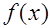
的最小正周期及解析式；
(2)设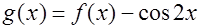
，求函数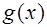
在区间 R上的最大值和最小值及对应的x的集合.
已知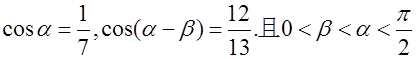
(Ⅰ)求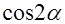
的值．
（Ⅱ）求
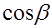的值．