设不等式组 所表示的平面区域为Dn,记Dn内整点的个数为an(横纵坐标均为整数的点称为整点).
所表示的平面区域为Dn,记Dn内整点的个数为an(横纵坐标均为整数的点称为整点).
(1)n=2时,先在平面直角坐标系中作出区域D2,再求a2的值;
(2)求数列{an}的通项公式;
(3)记数列{an}的前n项的和为Sn,试证明:对任意n∈N*,恒有 <
<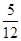 成立.
成立.
设命题p:f(x)= 在区间(1,+∞)上是减函数;命题q:x1,x2是方程x2-ax-2=0的两个实根,且不等式m2+5m-3≥|x1-x2|对任意的实数a∈[-1,1]恒成立.若
在区间(1,+∞)上是减函数;命题q:x1,x2是方程x2-ax-2=0的两个实根,且不等式m2+5m-3≥|x1-x2|对任意的实数a∈[-1,1]恒成立.若 p∧q为真,试求实数m的取值范围.
p∧q为真,试求实数m的取值范围.
已知集合A={x|1<ax<2},集合B={x||x|<1}.当A B时,求a的取值范围.
B时,求a的取值范围.
已知数列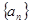 中,
中,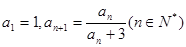
(1)求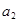 ,
,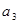 ;
;
(2)求证: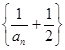 是等比数列,并求
是等比数列,并求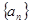 的通项公式
的通项公式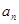 ;
;
(3)数列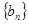 满足
满足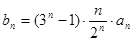 ,数列
,数列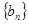 的前n项和为
的前n项和为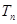 ,若不等式
,若不等式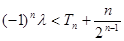 对一切
对一切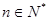 恒成立,求
恒成立,求 的取值范围.
的取值范围.
如图,渔船甲位于岛屿A的南偏西60°方向的B处,且与岛屿A相距12海里,渔船乙以10海里/时的速度从岛屿A出发沿正北方向航行,若渔船甲同时从B处出发沿北偏东α的方向追赶渔船乙,刚好用2小时追上,此时到达C处.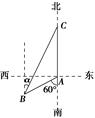
(1)求渔船甲的速度;
(2)求sinα的值.
已知数列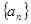 的前
的前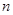 项和为
项和为 ,且2
,且2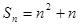 .
.
(1)求数列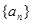 的通项公式;
的通项公式;
(2)若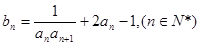 求数列
求数列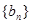 的前
的前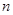 项和
项和 .
.