等腰Rt△ABC中,∠BAC=90°,点A、点B分别是x轴、y轴两个动点,直角边AC交x轴于点D,斜边BC交y轴于点E;
(1)如图(1),若A(0,1),B(2,0),求C点的坐标;
(2)如图(2),当等腰Rt△ABC运动到使点D恰为AC中点时,连接DE,求证:∠ADB=∠CDE
(3)如图(3),在等腰Rt△ABC不断运动的过程中,若满足BD始终是∠ABC的平分线,试探究:线段OA、OD、BD三者之间是否存在某一固定的数量关系,并说明理由.
在一个不透明的口袋中装有3个带号码的球,球号分别为2,3,4,这些球除号码不同外其它均相同。甲、乙、两同学玩摸球游戏,游戏规则如下:
先由甲同学从中随机摸出一球,记下球号,并放回搅匀,再由乙同学从中随机摸出一球,记下球号。将甲同学摸出的球号作为一个两位数的十位上的数,乙同学的作为个位上的数。若该两位数能被4整除,则甲胜,否则乙胜.
问:这个游戏公平吗?请说明理由。
如图,抛物线 与x轴交于C.A两点,与y轴交于点B,OB=4.点O关于直线AB的对称点为D,E为线段AB的中点.
与x轴交于C.A两点,与y轴交于点B,OB=4.点O关于直线AB的对称点为D,E为线段AB的中点.
(1)分别求出点A.点B的坐标;
(2)求直线AB的解析式;
(3)若反比例函数 的图象过点D,求k值;
的图象过点D,求k值;
(4)两动点P、Q同时从点A出发,分别沿AB.AO方向向B.O移动,点P每秒移动1个单位,点Q每秒移动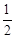 个单位,设△POQ的面积为S,移动时间为t,问:S是否存在最大值?若存在,求出这个最大值,并求出此时的t值;若不存在,请说明理由.
个单位,设△POQ的面积为S,移动时间为t,问:S是否存在最大值?若存在,求出这个最大值,并求出此时的t值;若不存在,请说明理由.
如图,⊙O的直径AB=4,C为圆周上一点,AC=2,过点C作⊙O的切线DC,P点为优弧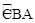 上一动点(不与A.C重合).
上一动点(不与A.C重合).
(1)求∠APC与∠ACD的度数;
(2)当点P移动到CB弧的中点时,求证:四边形OBPC是菱形.
(3)P点移动到什么位置时,△APC与△ABC全等,请说明理由.
阅读材料:对于任何实数,我们规定符号 的意义是
的意义是 =ad﹣bc.例如:
=ad﹣bc.例如: =1×4﹣2×3=﹣2,
=1×4﹣2×3=﹣2,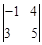 =(﹣2)×5﹣4×3=﹣22.
=(﹣2)×5﹣4×3=﹣22.
(1)按照这个规定,请你计算 的值;
的值;
(2)按照这个规定,请你计算:当x2﹣4x+4=0时, 的值.
的值.
某公园出售的一次性使用门票,每张10元,为了吸引更多游客,新近推出购买“个人年票”的售票活动(从购买日起,可供持票者使用一年).年票分A.B两类:A类年票每张100元,持票者每次进入公园无需再购买门票;B类年票每张50元,持票者进入公园时需再购买每次2元的门票.某游客一年中进入该公园至少要超过多少次时,购买A类年票最合算?