（本小题12分）如图，在平面直角坐标系xOy中，点P（a，b）在第一象限．以P为圆心的圆经过原点，与y轴的另一个交点为A．点Q是线段OA上的点（不与O，A重合），过点Q作PQ的垂线交⊙P于点B（m，n），其中m≥0．
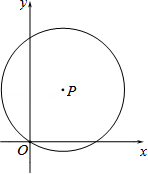
（1）若b=5，则点A坐标是 ；
（2）在（1）的条件下，若OQ=8，求线段BQ的长；
（3）若点P在函数y=x2（x＞0）的图象上，△BQP是等腰三角形且PQ=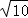
求出点B的坐标．
有一个函数图像经过下列各点：(-2，3)，(-1，0)，(0，-1)，(1，0)，(2，3).
（1）请你描述该函数图像；
（2）写出两个变量间的函数关系式；
（3）你能通过表格的形式，列出两个变量的对应值，使两个变量间的关系满足(2)中的关系式吗?
在一个函数中的两个变量的对应值如下表：请你通过画图像，写出两个变量间的关系式.
| x |
-2 |
-1 |
0 |
1 |
2 |
… |
| y |
3 |
0 |
-1 |
0 |
3 |
… |
一个运动员练习推铅球，铅球刚出手时，离地面
米，铅球落地点离铅球刚出手时相应的地面的点10米，铅球运行中最高点离地面3米，已知铅球走过的路线是抛物线，求该抛物线的函数关系式.
如图，△ABC是边长为4的等边三角形，P是BC上的点，PD∥AC交AB于D，PE∥AB交AC于E，设PB为x，四边形ADPE的面积为y.求y与x之间的函数关系式.
正方形的周长为L，面积为S，用L表示出函数S的关系式.