按如图所示的程序计算,若开始输入的x的值为48,我发现第一次得到的结果为24,第二次得到的结果为12,…,请你探索: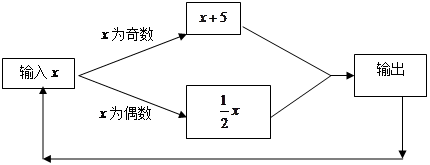
(1)第四次得到的结果;(2)第九次得到的结果;(3)第2012次得到的结果.
若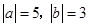 ,①求
,①求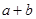 的值;②若
的值;②若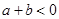 ,求
,求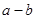 的值.
的值.
有20筐白菜,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
| 与标准质量的差值 (单位:千克) |
 3 3 |
 2 2 |
 1.5 1.5 |
0 |
1 |
2.5 |
| 筐数 |
1 |
4 |
2 |
3 |
2 |
8 |
(1)20筐白菜中,最重的一筐比最轻的一筐重 千克;
(2)与标准重量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价2.6元,则出售这20筐白菜可卖多少元?
我们定义一种新运算: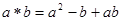 .
.
(1)求 的值;(2)求
的值;(2)求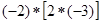 的值.
的值.
已知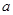 、
、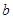 互为相反数且
互为相反数且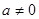 ,
,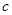 、
、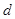 互为倒数,
互为倒数,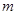 的绝对值是最小的正整数,
的绝对值是最小的正整数,
求 的值.(注:
的值.(注: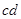 =
=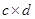 )
)
解:∵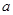 、
、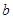 互为相反数且
互为相反数且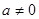 ,∴
,∴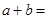 ,
,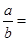 ;
;
又∵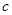 、
、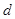 互为倒数,∴
互为倒数,∴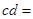 ;
;
又∵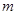 的绝对值是最小的正整数, ∴
的绝对值是最小的正整数, ∴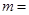 ,∴
,∴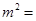 ;
;
∴原式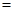 .
.