如图,用长为20米的篱笆恰好围成一个扇形花坛,且扇形花坛的圆心角小于180°,设扇形花坛的半径为r米,面积为S平方米.(注: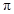 的近似值取3)
的近似值取3)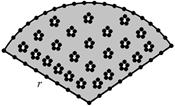
(1)求出S与r的函数关系式,并写出自变量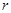 的取值范围;
的取值范围;
(2)当半径r为何值时,扇形花坛的面积最大,并求面积的最大值.
如图,AB是⊙O的弦,OC⊥AB于点C,连接OA,AB=12,⊙O半径为10.
(1)求OC的长;
(2)点E,F在⊙O上,EF∥AB.若EF=16,直接写出EF与AB之间的距离.
已知:二次函数y=x2+bx-3的图象经过点A(2,5).
(1)求二次函数的解析式;
(2)求二次函数的图象与x轴的交点坐标;
(3)将(1)中求得的函数解析式用配方法化成y=(x-h)2+k的形式.
(本题12分)如图,已知直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,AB=8,CD=10.
(1)求梯形ABCD的面积;
(2)动点P从点B出发,以2个单位/s的速度沿B→A→D→C方向向点C运动;动点Q从点C出发,以2个单位/s的速度沿C→D→A方向向点A运动;过点Q作QE⊥BC于点E.若P、Q两点同时出发,当其中一点到达终点时另一点也随之停止运动,设运动时间为t秒.问:
①当点P在B→A上运动时,是否存在这样的t,使得直线PQ将梯形ABCD的周长平分?若存在,请求出t的值,并判断此时PQ是否平分梯形ABCD的面积;若不存在,请说明理由.
②在运动过程中,是否存在这样的t,使得以P、D、Q为顶点的三角形恰好是以DQ为一腰的等腰三角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.
阅读材料:
例:说明代数式 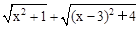 的几何意义,并求它的最小值.
的几何意义,并求它的最小值.
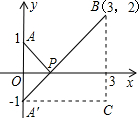
解: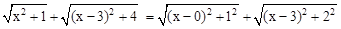 ,如图,建立平面直角坐标系,点P(x,0)是x轴上一点,则
,如图,建立平面直角坐标系,点P(x,0)是x轴上一点,则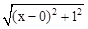 可以看成点P与点A(0,1)的距离,
可以看成点P与点A(0,1)的距离,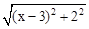 可以看成点P与点B(3,2)的距离,所以原代数式的值可以看成线段PA与PB长度之和,它的最小值就是PA+PB的最小值.
可以看成点P与点B(3,2)的距离,所以原代数式的值可以看成线段PA与PB长度之和,它的最小值就是PA+PB的最小值.
设点A关于x轴的对称点为A′,则PA=PA′,因此,求PA+PB的最小值,只需求PA′+PB的最小值,而点A′、B间的直线段距离最短,所以PA′+PB的最小值为线段A′B的长度.为此,构造直角三角形A′CB,因为A′C=3,CB=3,所以A′B=3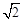 , 即原式的最小值为3
, 即原式的最小值为3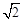 .
.
根据以上阅读材料,解答下列问题:
(1)代数式 的值可以看成平面直角坐标系中点P(x,0)与点A(1,1)、点B的距离之和.(填写点B的坐标)
的值可以看成平面直角坐标系中点P(x,0)与点A(1,1)、点B的距离之和.(填写点B的坐标)
(2)代数式  的最小值.
的最小值.