如图,直线y =" 2x" + 3与x轴相交于点A,与y轴相交于点B.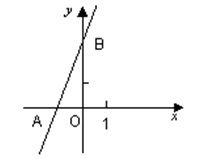
(1)求A,B两点的坐标;
(2)过B点作直线BP与x轴的正半轴相交于P,且使OP = 2OA,求ΔABP的面积.
一个不透明的袋子里装有编号分别为1、2、3的球(除编号以为,其余都相同),其中1号球1个,3号球3个,从中随机摸出一个球是2号球的概率为 .
.
(1)求袋子里2号球的个数.
(2)甲、乙两人分别从袋中摸出一个球(不放回),甲摸出球的编号记为x,乙摸出球的编号记为y,用列表法求点A(x,y)在直线y=x下方的概率.
甲、乙两校参加如皋市教育局举办的学生英语口语竞赛,两校参赛人数相等.比赛结束后,发现学生成绩分别为7分、8分、9分、10分(满分为10分).依据统计数据绘制了如下尚不完整的统计图表.
| 分 数 |
7 分 |
8 分 |
9 分 |
10 分 |
| 人 数 |
11 |
0 |
8 |

(1)在图1中,“7分”所在扇形的圆心角等于_________;
(2)请你将图2的统计图补充完整;
(3)经计算,乙校的平均分是8.3分,中位数是8分,请写出甲校的平均分、中位数;并从平均分和中位数的角度分析哪个学校成绩较好;
(4)如果教育局要组织8人的代表队参加省级团体赛,为便于管理,决定从这两所学校中的一所挑选参赛选手,请你分析,应选哪所学校?
先化简,再求值: 其中
其中 是方程
是方程 的根.
的根.
如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一动点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.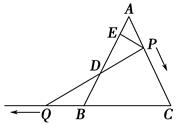
(1)当∠BQD=30°时,求AP的长;
(2)在运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.
如图,在△ABC中,AB=AC,AD⊥BC于点D,将△ADC绕点A顺时针旋转,使AC与AB重合,点D落在点E处,AE的延长线交CB的延长线于点M,EB的延长线交AD的延长线于点N.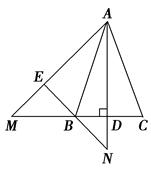
求证:AM=AN.