（本 题14分）已知矩形ABCD的顶点A与点O重合，AD、AB分别在x轴、y轴上，且AD=2，AB=3；抛物线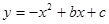
经过坐标原点O和x轴上另一点E（4，0）。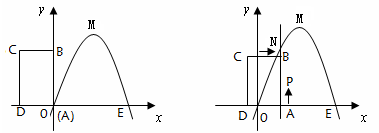
（1）当x取何值时，该抛物线的最大值是多少？
（2）将矩形ABCD以每秒1个单位长度的速度从图1所示的位置沿x轴的正方向匀速平行移动，同时一动点P也以相同的速度从点A出发向B匀速移动.设它们运动的时间为t秒（0≤t≤3），直线AB与该抛物线的交点为N（如图2所示）。
① 当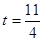
时，判断点P是否在直线ME上，并说明理由；
② 以P、N、C、D为顶点的多边形面积是否可能为5，若有可能，求出此时N点的坐标；若无可能，请说明理由．
本市出租车的收费标准为：3千米以内（含3千米）收费5元，超过3千米的部分每千米收费1．20元（不足1千米按1千米计算），另加收0．60元的返空费．
（1）设行驶路程为x千米（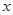
≥3且取整数），用x表示出应收费y元的代数式；
（2）当收费为10．40元时，该车行驶路程不超过多少千米？路程数在哪个范围内？
某公园欲建如图13-2-3所示形状的草坪（阴影部分），求需要铺设草坪多少平方米？若每平方米草坪需120元，则为修建该草坪需投资多少元？（单位：米）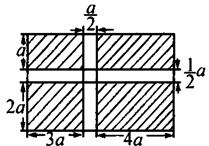
求下列分式的值：
（1）
其中a＝3．
（2）
其中x＝2，y＝－1．
x为何值时，分式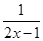
与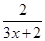
的值相等？并求出此时分式的值．
（1）已知分式
，x取什么值时，分式的值为零？
（2）x为何值时，分式
的值为正数？