如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=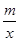 (m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(-2,0),且tan∠ACO=2.
(m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(-2,0),且tan∠ACO=2. 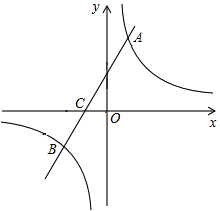
(1)求该反比例函数和一次函数的解析式;
(2)求点B的坐标;
(3)在x轴上求点E,使△ACE为直角三角形.(直接写出点E的坐标)
在兰州市开展的“体育、艺术2+1”活动中,某校根据实际情况,决定主要开设A:乒乓球,B:篮球,C:跑步,D:跳绳这四种运动项目.为了解学生喜欢哪一种项目,随机抽取了部分学生进行调查,并将调查结果绘制成如图甲、乙所示的条形统计图和扇形统计图.请你结合图中的信息解答下列问题: 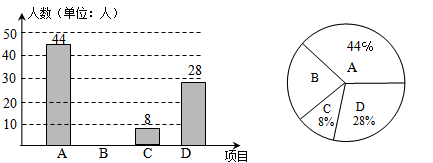
(1)样本中喜欢B项目的人数百分比是,其所在扇形统计图中的圆心角的度数是;
(2)把条形统计图补充完整;
(3)已知该校有1000人,根据样本估计全校喜欢乒乓球的人数是多少?
甲、乙两名学生练习计算机打字,甲打一篇1000字的文章与乙打一篇900字的文章所用的时间相同.已知甲每分钟比乙每分钟多打5个字.问:甲、乙两人每分钟各打多少字?
(1)已知:如图1,在矩形ABCD中,点E,F分别在AB,CD边上,BE=DF,连接CE,AF.求证:AF=CE.
(2)如图2,AB切⊙O于点B,OA=2,∠OAB=30°,弦BC∥OA.求:劣弧BC的长.(结果保留π)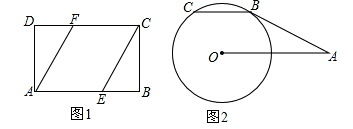
(1)解不等式:x-6>3x+2
(2)解方程组: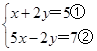 .
.