（本题8分）某文具店销售一种进价为每本10元的笔记本，为获得高利润，以不低于进价进行销售，结果发现，每月销售量
与销售单价
之间的关系可以近似地看作一次函数：
，物价部门规定这种笔记本每本的销售单价不得高于18元.
（1）当每月销售量为70本时，获得的利润为多少元？
（2）该文具店这种笔记本每月获得利润为
元，求每月获得的利润元与销售单价之间的函数关系式，并写出自变量的取值范围.
（3）当销售单价定为多少元时，每月可获得最大利润，最大利润为多少元？
面对全球金融危机的挑战，我国政府毅然启动内需，改善民生．国务院决定从2009年2月1日起，“家电下乡”在全国范围内实施，农民购买人选产品，政府按原价购买总额的13%给予补贴返还．某村委会组织部分农民到商场购买人选的同一型号的冰箱、电视机两种家电，已知购买冰箱的数量是电视机的2倍，且按原价购买冰箱总额为40000元、电视机总额为15000元．根据“家电下乡”优惠政策，每台冰箱补贴返还的金额比每台电视机补贴返还的金额多65元，求冰箱、电视机各购买多少台？
（1）设购买电视机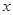
台，依题意填充下列表格：
 项目家电种类 |
购买数量（台） |
原价购买总额（元） |
政府补贴返还比例 |
补贴返还总金额（元） |
每台补贴返还金额（元） |
| 冰箱 |
40 000 |
13% |
|||
| 电视机 |
|
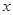15 000 |
13% |
（2）列出方程（组）并解答．
如图，平行四边形ABCD中，AB＝5，BC＝10，BC边上的高AM=4，E为 BC边上的一个动点（不与B、C重合）．过E作直线AB的垂线，垂足为F． FE与DC的延长线相交于点G，连结DE，DF．.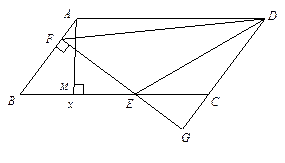
求证：ΔBEF ∽ΔCEG．
当点E在线段BC上运动时，△BEF和△CEG的周长之间有什么关系？并说明你的理由．
设BE＝x，△DEF的面积为 y，请你求出y和x之间的函数关系式，并求出当x为何值时,y有最大值，最大值是多少？
在图1至图3中，点B是线段AC的中点，点D是线段CE的中点．四边形BCGF和CDHN都是正方形．AE的中点是M．
如图1，点E在AC的延长线上，点N与点G重合时，点M与点C重合，
求证：FM = MH，FM⊥MH将图-1中的CE绕点C顺时针旋转一个锐角，得到图2，
求证：△FMH是等腰直角三角形将图2中的CE缩短到图3的情况，△FMH还是等腰直角三角形吗？（不必
说明理由）
已知：如图，在
△ABC中，∠ABC＝90°，以AB上的点O为圆心，OB的长为半径的圆与AB交于点E，与AC切于点D．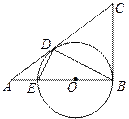
求证：BC＝CD；
求证：∠ADE＝∠ABD；
设AD＝2，AE＝1，求⊙O直径的长．
某天，小明来到体育馆看球赛，进场时，发现门票还在家里，此时离比赛开始还有25分钟，于是立即步行回家取票.同时，他父亲从家里出发骑自行车以他3倍的速度给他送票，两人在途中相遇，相遇后小明立即坐父亲的自行车赶回体育馆.下图中线段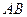
、
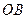分别表示父、子俩送票、取票过程中，离体育馆的路程
（米）与所用时间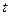
（分钟）之间的函数关系，结合图象解答下列问题（假设骑自行车和步行的速度始终保持不变）：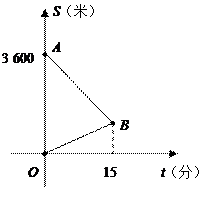
求点
的坐标和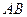所在直线的函数关系式小明能否在比赛开始前到达体育馆