(本小题满分12分)合肥一中生活区内建有一块矩形休闲区域ABCD,AB=100米,BC=50 米,为了便于同学们平时休闲散步,学校后勤部门将在这块区域内铺设三条小路OE、EF和OF,考虑到学校整体规划,要求O是AB的中点,点E在边BC上,点F在边AD上,且OE⊥OF,如图所示.
米,为了便于同学们平时休闲散步,学校后勤部门将在这块区域内铺设三条小路OE、EF和OF,考虑到学校整体规划,要求O是AB的中点,点E在边BC上,点F在边AD上,且OE⊥OF,如图所示.
(1)设∠BOE=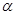 ,试将△OEF的周长L表示成
,试将△OEF的周长L表示成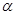 的函数关系式,并求出此函数的定义域;
的函数关系式,并求出此函数的定义域;
(2)经核算,三条路每米铺设费用均为800元,试问如何设计才能使铺路的总费用最低?并求出最低总费用.
已知函数f(x)= ,x∈[1,+∞).
,x∈[1,+∞).
(1)当a=4时,求函数f(x)的最小值;
(2)若对任意x∈[1,+∞),f(x)>0恒成立,试求实数a的取值范围.
(1)已知x<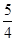 ,求函数y=4x-2+
,求函数y=4x-2+ 的最大值;
的最大值;
(2)已知x>0,y>0且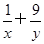 =1,求x+y的最小值.
=1,求x+y的最小值.
(1)若a>b>c,求证: ;
;
(2)若a>b>c,求使得 恒成立的k的最大值.
恒成立的k的最大值.
已知x>0,y>0,求证: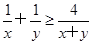 .
.
某营养师要为某个儿童预订午餐和晚餐.已知一个单位的午餐含12个单位的碳水化合物、6个单位的蛋白质和6个单位的维生素C;一个单位的晚餐含8个单位的碳水化合物、6个单位的蛋白质和10个单位的维生素C.另外,该儿童这两餐需要的营养中至少含64个单位的碳水化合物、42个单位的蛋白质和54个单位的维生素C.
如果一个单位的午餐、晚餐的费用分别是2.5元和4元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预订多少个单位的午餐和晚餐?