如图 ,在
,在 中,
中, °,
°, ,
,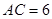 ,
, ,
, 分别是
分别是 ,
,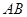 上的点,且
上的点,且 ,
, ,将
,将 沿
沿 折起到
折起到 的位置,使
的位置,使 ,如图
,如图 .
.
(Ⅰ)求证: 平面
平面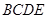 ;
;
(Ⅱ)若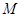 是
是 的中点,求
的中点,求 与平面
与平面 所成角的大小;
所成角的大小;
(Ⅲ)点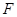 是线段
是线段 的靠近点
的靠近点 的三等分点,点
的三等分点,点 是线段
是线段 上的点,直线
上的点,直线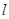 过点
过点 且垂直于平面
且垂直于平面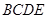 ,求点
,求点 到直线
到直线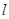 的距离的最小值.
的距离的最小值.
已知圆C: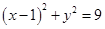 内有一点P(2,2),过点P作直线l交圆C于A、B两点.
内有一点P(2,2),过点P作直线l交圆C于A、B两点.
(1)当弦AB被点P平分时,写出直线l的方程;
(2)当直线l的倾斜角为45º时,求弦AB的长.
如图,在四棱锥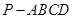 中,底面
中,底面 是矩形,已知
是矩形,已知 ,
,
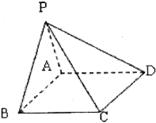
(1)证明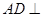 平面
平面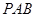 ;
;
(2)求异面直线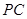 与
与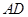 所成的角的正切值;
所成的角的正切值;
(3)求四棱锥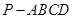 的体积。
的体积。
已知直线 经过两点A(2,1),B(6,3)
经过两点A(2,1),B(6,3)
(1)求直线 的方程
的方程
(2)圆C的圆心在直线 上,并且与
上,并且与 轴相切于点(2,0),求圆C的方程
轴相切于点(2,0),求圆C的方程
(3)若过B点向(2)中圆C引切线BS、BT,S、T分别是切点,求ST直线的方程.
如图所示,在直三棱柱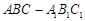 中,
中,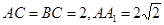 ,∠ACB=90°,M是
,∠ACB=90°,M是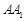 的中点,N是
的中点,N是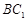 的中点
的中点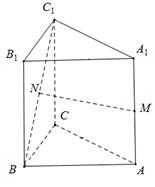
(Ⅰ)求证:MN∥平面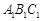 ;
;
(Ⅱ)求点 到平面BMC的距离;
到平面BMC的距离;
如图,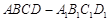 为正方体,下面结论错误的是
为正方体,下面结论错误的是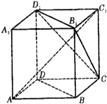
A.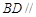 平面 平面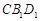 |
B.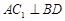 |
C.平面ACC1A1⊥平面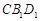 |
D.异面直线 与 与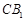 所成的角为60° 所成的角为60° |