(本小题满分10分)袋中装有大小相同的黑球和白球共9个,从中任取2个都是白球的概率为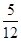 .现甲、乙两人从袋中轮流摸球,甲先取,乙后取,然后甲再取 ,每次摸取1个球,取出的球不放回,直到其中有一人取到白球时终止.用X表示取球终止时取球的总次数.
.现甲、乙两人从袋中轮流摸球,甲先取,乙后取,然后甲再取 ,每次摸取1个球,取出的球不放回,直到其中有一人取到白球时终止.用X表示取球终止时取球的总次数.
(1)求袋中原有白球的个数;
(2)求随机变量X的概率分布及数学期望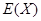 .
.
如图,直棱柱
中,
分别是
的中点,
.

(Ⅰ)证明:
平面
;
(Ⅱ)求二面角
的正弦值.
在内角
的对边分别为
,已知
.
(Ⅰ)求
;
(Ⅱ)若
,求
面积的最大值.
已知双曲线
的左、右焦点分别为
离心率为 直线
与
的两个交点间的距离为
直线
与
的两个交点间的距离为
(I)求
;
(II)设过
的直线
与
的左、右两支分别相交有
两点,且
证明:
成等比数列
已知函数 .
(I)当
时,讨论
的单调性;
(II)若
时,
,求
的取值范围.
甲、乙、丙三人进行羽毛球练习赛,其中两人比赛,另一人当裁判,每局比赛结束时,负的一方在下一局当裁判,设各局中双方获胜的概率均为
各局比赛的结果都相互独立,第 局甲当裁判.
局甲当裁判.
(I)求第 局甲当裁判的概率;
局甲当裁判的概率;
(II)求前 局中乙恰好当
局中乙恰好当 次裁判概率.
次裁判概率.