如图所示，两带电平行金属板A、B与竖直方向成30°角放置，两板间电势差
=500V。B板中心有一小孔正好位于平面直角坐标系 xOy上的O点，y轴沿竖直方向。一比荷为1.0×105C/kg的带正电粒子P，从A板中心
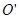处静止释放后沿垂直于金属板的直线
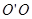进入x轴下方第四象限的匀强电场E中，场强方向与AB板平行且斜向上。粒子穿过电场后，从坐标P（1m，0）处离开电场，粒子的重力不计（如有需要：
、
、
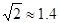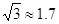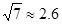）。试求：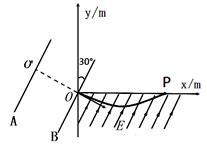
（1）粒子刚进入匀强电场时的速度大小；
（2）匀强电场的场强E的大小；
（3）求粒子离开电场时的速度大小；
如图所示的电路中，电压表为理想表，电阻R＝10 Ω，当开关S断开时，电压表示数为6 V，当开关S闭合时，电压表示数为5 V，则电源的内阻为多少？
如图所示，在半径为
的圆形区域内有水平向里的匀强磁场，磁感应强度B，圆形区域右侧有一竖直感光板，从圆弧顶点P以速率
的带正电粒子平行于纸面进入磁场，已知粒子的质量为m，电量为q，粒子重力不计。
⑴若粒子对准圆心射入，求它在磁场中运动的时间；
⑵若粒子对准圆心射入，且速率为
，求它打到感光板上时速度的垂直分量；
⑶若粒子以速度从P点以任意角入射，试证明它离开磁场后均垂直打在感光板上。
光滑水平面上有质量为M、高度为h的光滑斜面体A，斜面上有质量为m的小物体B，都处于静止状态。从某时刻开始释放物体B，在B沿斜面下滑的同时斜面体A沿水平方向向左做匀加速运动。经过时间t，斜面体水平移动s，小物体B刚好滑到底端。
（1）求运动过程中斜面体A所受的合力
；
（2）分析小物体B做何种运动？并说明理由；
（3）求小物体B到达斜面体A底端时的速度
大小。
(4分) 一质量为0.5kg的小球A以2.0m/s的速度和静止于光滑水平面上质量为1kg的另一大小相等的小球B发生正碰，碰撞后它以0.2m/s的速度反弹。求（1）原来静止小球获得的速度大小；（2）碰撞过程中损失的机械能。
(4分)半球形介质截面如图所示，O为圆心，单色光a、b相互平行，从不同位置进入介质，光线a在O点恰好产生全反射。光线b的入射角为45°，求：（1）介质的折射率；（2）光线b在介质中的折射角。