如图所示,带电平行金属板相距为2R,在两板间有垂直纸面向里、磁感应强度为B的圆形匀强磁场区域,与两板及左侧边缘线相切。一个带正电的粒子(不计重力)沿两板间中心线O1O2从左侧边缘O1点以某一速度射入,恰沿直线通过圆形磁场区域,并从极板边缘飞出,在极板间运动时间为t0。若撤去磁场,粒子仍从O1点以相同速度射入,则经t0/2时间打到极板上。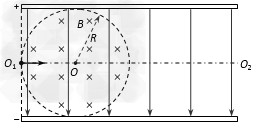
(1)求极板长度L和粒子的初速度v0;
(2)求两极板间电压U和粒子的比荷q/m;
(3)若两极板不带电,保持磁场不变,该粒子仍沿中心线O1O2从O1点射入,欲使粒子从两板间飞出,求射入的速度应满足条件。(已知tan2θ =2tanθ/(1-tan2θ)
如图甲所示,是一位同学在实验室中照的一小球做平抛运动的频闪照片的一部分,由于照相时的疏忽,没有摆上背景方格板,图中方格是后来用直尺画在相片上的(图中格子的竖直线是实验中重垂线的方向,每小格的边长均为5mm ) ,为了补救这一过失,他对小球的直径进行了测量,如图乙所示,如果取重力加速度g=10m/s 2,则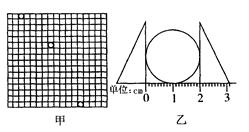
(1)频闪照片闪光的频率为 _____Hz;
(2)小球作平抛运动的初速度为____m/s。
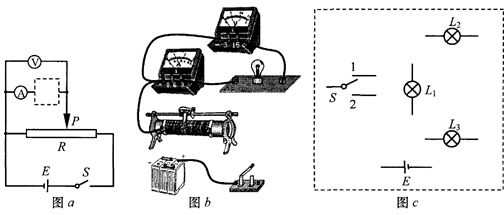
有一只电压表,量程已知,内阻为RV,另有一蓄电池(电动势未知,但不超过电压表的量程,内阻可忽略),请用这只电压表和蓄电池,再用一个单刀双掷开关和一些连接导线,设计测量某一高值电阻Rx的实验方法(已知Rx的值与RV相差不大)。
(1)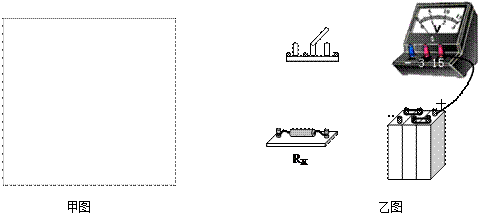 在甲图的方框内,画出实验电路图;
在甲图的方框内,画出实验电路图;
(2)请用笔画线代替导线连接如图乙所示的实物图(其中部分已连好);
(3)简要写出实验的主要步骤,并根据实验测得的数据,推导出高值电阻Rx的表达式。
某实验小组利用如图甲所示的实验装置来验证钩码和滑块所组成的系统由静止释放后机械能是否守恒。实验前已经调整气垫导轨底座使之水平,且选定滑块从静止开始运动的过程进行测量。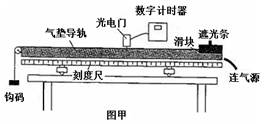
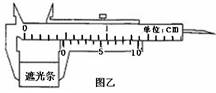
(1)如图乙所示,用游标卡尺测得窄遮光条的宽度d=______cm;实验时将滑块从图示位置由静止释放,由数字计时器读出遮光条通过光电门的时间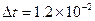 s,则在遮光条经过光电门时滑块的瞬间速度为_______m/s。(计算结果保留两位有效数字)
s,则在遮光条经过光电门时滑块的瞬间速度为_______m/s。(计算结果保留两位有效数字)
(2)已知当地重力加速度为g,钩码的质量为m,滑块的质量为M,在本实验中还需要直接测量的物理量有:________(在横线上填入选项前的编号)。
①光电门到导轨左端定滑轮的距离x
②滑块上的遮光条初始位置到光电门的距离s
③气垫导轨的总长L
(3)本实验通过比较________和 是否相等(用直接测出的物理量符号写出表达式,重力加速度为g)说明系统的机械能是否守恒。
是否相等(用直接测出的物理量符号写出表达式,重力加速度为g)说明系统的机械能是否守恒。
(4)为提高实验结果的准确程度,该实验小组的同学对此实验提出以下建议,其中确实对提高准确程度有作用的是_____。(在横线上填入选项前的编号)
①绳的质量要轻,滑块与滑轮间绳要水平
②在“轻质绳”的前提下,绳越长越好
③钩码的质量m越小越好
某同学利用图(a)所示的电路研究灯泡L1(6V,1.5W)、L2(6V,10W)的发光情况(假设灯泡电阻恒定),图(b)为实物图。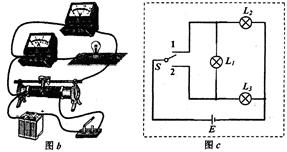
 |
(1)他分别将L1、L2接入图(a)中的虚线框位置,移动滑动变阻器的滑片P,当电压表示数为6V时,发现灯泡均能正常发光。在图(b)中用笔线代替导线将电路连线补充完整。
(2)接着他将L1和L2串联后接入图(a)中的虚线框位置,移动滑动变阻器的滑片P,当电压表示数为6V时,发现其中一个灯泡亮而另一个灯泡不亮,出现这种现象的原因是_____________________________。
(3)现有如下器材:电源E(6V,内阻不计),灯泡L1(6V,1.5W)、L2(6V,10W),L3(6V,10W),单刀双掷开关S。在图(c)中设计一个机动车转向灯的控制电路:当单刀双掷开关S与1相接时,信号灯L1亮,右转向灯L2亮而左转向灯L3不亮;当单刀双掷开关S与2相接时,信号灯L1亮,左转向灯L3亮而右转向灯L2不亮。
把两个大小相同、质量不等的金属球用细线连接,中间夹一被压缩了的轻弹簧,置于光滑的水平桌面上,如图所示.烧断细线,观察两球的运动情况,进行必要的测量,验证物体间相互作用时动量守恒.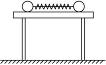
(1)还必须添加的器材是:_____________________________________________________.
(2)需直接测量的数据是:_____________________________________________________.
(3)用所得数据验证动量守恒定律的关系式是_____________________________________.