有一只电压表,量程已知,内阻为RV,另有一蓄电池(电动势未知,但不超过电压表的量程,内阻可忽略),请用这只电压表和蓄电池,再用一个单刀双掷开关和一些连接导线,设计测量某一高值电阻Rx的实验方法(已知Rx的值与RV相差不大)。
(1)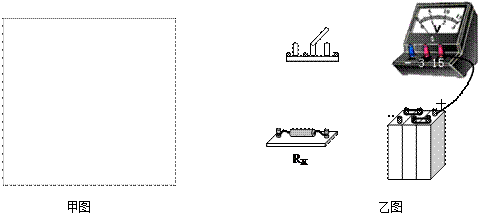 在甲图的方框内,画出实验电路图;
在甲图的方框内,画出实验电路图;
(2)请用笔画线代替导线连接如图乙所示的实物图(其中部分已连好);
(3)简要写出实验的主要步骤,并根据实验测得的数据,推导出高值电阻Rx的表达式。
如图所示,一质量为m =" 0.5" kg的小滑块,在F =" 4" N水平拉力的作用下,从水平面上的A处由静止开始运动,滑行s =" 1.75" m后由B处滑上倾角为37°的光滑斜面,滑上斜面后拉力的大小保持不变,方向变为沿斜面向上,滑动一段时间后撤去拉力。已知小滑块沿斜面上滑到的最远点C距B点为L =" 2" m,小滑块最后恰好停在A处。不计B处能量损失,g取10 m/s2,已知sin37° = 0.6 cos37° = 0.8。试求: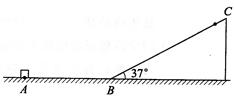
(1)小滑块与水平面间的动摩擦因数μ。
(2)小滑块在斜面上运动时,拉力作用的距离x。
(3)小滑块在斜面上运动时,拉力作用的时间t。
质量为2kg的平板车B上表面水平且车长为2.5m,原来静止在光滑水平面上,平板车一端静止着一块质量为2kg的物体A,一颗质量为0.01kg的子弹以700m/s的速度水平瞬间射穿A后,速度变为l00m/s,如果A与B之间的动摩擦因数为0.05,且子弹和物体A均可视为质点,重力加速度为g取10m/s2.求: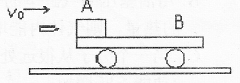
①A在平板车上运动的最大速度;
②A从B上滑离时,A和B的速度.
如图所示,OBCD为半圆柱体玻璃的横截面,OD为直径,一束由红光和紫光组成的复色光沿AO方向从真空斜射入玻璃,B、C点为两单色光的射出点(设光线在B、C处未发生全反射).已知从B点射出的单色光由O到B的传播时间为t。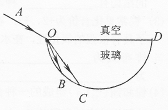
①若OB、OC两束单色光在真空中的波长分别为λB、λC,试比较λB、λC的大小(不必说明理由);
②求从C点射出的单色光由O到C的传播时间tC是多少?
如图所示,一定质量的理想气体被活塞封闭在可导热的气缸内,活塞相对于底部的高度为h,可沿气缸无摩擦地滑动.取质量为m的沙子缓慢地倒在活塞的上表面上。沙子倒完时,活塞下降了h/4,再取一定质量的沙子缓慢地倒在活塞的上表面上。外界大气的压强和温度始终保持不变,此次沙子倒完时活塞距气缸底部的高度为h/2.求第二次倒入活塞上的沙子的质量。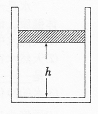
如图,在xoy平面上x<0的区域内存在一垂直纸面向外的匀强磁场,磁感应强度大小为B;OA是过原点的一条直线,与y轴正方向夹角为60°.在x>0的区域有一与OA平行的匀强电场,场强大小为E.现有一质量为m,电量为q的带正电的粒子(重力不计)从直线OA上的某处P点由静止释放后,经0点进入磁场,经过一段时间后恰能垂直OA到达0A上的Q点(电场方向以及P点、Q点位置在图中均未画出).求
(1)P点的坐标;
(2)粒子从P点释放到垂直0A到达Q点所用的时间;
(3)PQ之间的距离.