(本小题满分12分)数列 的各项均为正数,
的各项均为正数,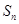 为其前n项和,对于任意的
为其前n项和,对于任意的 ,总有
,总有 成等差数列.
成等差数列.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设数列 前n项和为
前n项和为 ,且
,且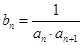 ,求证:
,求证: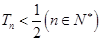 .
.
已知函数
(1)若 求
求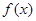 的值;
的值;
(2)求函数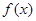 最小正周期及单调递减区间.
最小正周期及单调递减区间.
设命题 :实数x满足
:实数x满足 ,其中
,其中 ,命题
,命题 实数
实数 满足
满足 .
.
(Ⅰ)若 且
且 为真,求实数
为真,求实数 的取值范围;
的取值范围;
(Ⅱ)若 是
是
 的充分不必要条件,求实数
的充分不必要条件,求实数 的取值范围.
的取值范围.
已知函数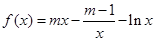 ,
,  在
在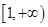 上为增函数,且
上为增函数,且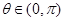 ,求解下列各题:
,求解下列各题:
(1)求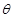 的取值范围;
的取值范围;
(2)若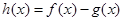 在
在 上为单调增函数,求
上为单调增函数,求 的取值范围;
的取值范围;
(3)设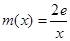 ,若在
,若在 上至少存在一个
上至少存在一个 ,使得
,使得 成立,求
成立,求 的取值范围.
的取值范围.
设函数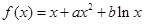 ,其对应的图像为曲线C;若曲线C过
,其对应的图像为曲线C;若曲线C过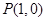 ,且在
,且在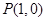 点处的切斜线率
点处的切斜线率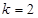
(1)求函数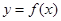 的解析式
的解析式
(2)证明不等式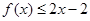 .
.
在每年的春节后,某市政府都会发动公务员参与到植树活动中去.为保证树苗的质量,该市林管部门在植树前,都会在植树前对树苗进行检测.现从甲乙两种树苗中各抽测了10株树苗的高度,量出树苗的高度如下(单位:厘米):
甲: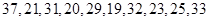
乙: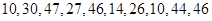
(1)根据抽测结果,完成答题卷中的茎叶图,并根据你填写的茎叶图,对甲、乙两种树苗的高度作比较,写出两个统计结论;
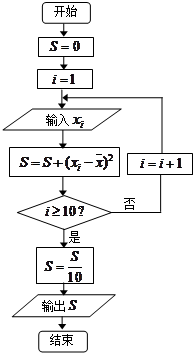
(2)设抽测的10株甲种树苗高度平均值为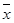 ,将这10株树苗的高度依次输入按程序框图进行的运算,问输出的
,将这10株树苗的高度依次输入按程序框图进行的运算,问输出的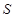 大小为多少?并说明
大小为多少?并说明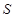 的统计学意义.
的统计学意义.