如图所示,固定于同一条竖直线上的A.B是两个带等量异种电荷的点电荷,电荷量分别为+Q和-Q,A.B相距为2d。MN是竖直放置的光滑绝缘细杆,另有一个穿过细杆的带电小球p,其质量为m、电荷量为+q(可视为点电荷,不影响电场的分布),现将小球p从与点电荷A等高的C处由静止开始释放,小球p向下运动到距C点距离为d的O点时,速度为v,已知MN与AB之间的距离为d,静电力常量为k,重力加速度为g.求: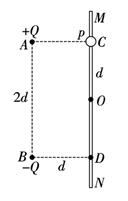
(1)C.O间的电势差UCO;
(2)小球p在O点时的加速度;
(3)小球p经过与点电荷B等高的D点时的速度.
两颗卫星在同一轨道平面绕地球做匀速圆周运动,地球半径为R,a卫星离地面的高度等于R,a卫星离地面高度为3R,则
(1)a、b两卫星周期之比Ta∶Tb是多少?
(2)若某时刻两卫星正好同时通过地面同一点的正上方,则a至少经过多少个周期两卫星相距最远?
在如图所示的圆锥摆中,已知绳子长度为L ,绳子转动过程中与竖直方向的夹角为θ ,试求小球做圆周运动的周期。
如图所示,在内壁光滑的平底试管内放一个质量为m=10g的小球, 试管的开口端加盖与水平轴O连接. 试管底与O相距L="5cm," 试管在转轴带动下沿竖直平面做匀速圆周运动。g取10m/s ,求:
,求:
(1)小球从最低点到最高点过程,重力对小球做的功及小球重力势能的变化量;
(2)转轴的角速度达到多大时, 试管底所受压力的最大值等于最小值的3倍;
(3)转轴的角速度满足什么条件时,会出现小球与试管底脱离接触的情况。
我国执行首次载人航天飞行的神州五号飞船于2003年10月15日在中国酒泉卫星发射中心发射升空.飞船由长征-2F运载火箭先送入近地点为A、远地点为B的椭圆轨道,在B点实施变轨后,再进入预定圆轨道,如图所示。已知飞船在预定圆轨道上飞行n圈所用时间为t,近地点A距地面高度为h1,地球表面重力加速度为g,地球半径为R,求:
(1)地球的第一宇宙速度大小;
(2)飞船在近地点A的加速度aA大小;
(3)远地点B距地面的高度h2大小。
如图,小球a、b用等长细线悬挂于同一固定点O。让球a静止下垂,将球b向右拉起,使细线水平。从静止释放球b,两球碰后粘在一起向左摆动,此后细线与竖直方向之间的最大偏角为60°。忽略空气阻力,求
(i)两球a、b的质量之比;
(ii)两球在碰撞过程中损失的机械能与球b在碰前的最大动能之比。